 |
 |
| Korean J Anesthesiol > Volume 71(3); 2018 > Article |
|
Abstract
Notes
1) The term “event” refers to the one of two responses of the binary categorical outcome variable; for example, “death” in the death or survival outcome of a patient and “remission” in the recurrence or remission outcome of back pain. The term “initial event” refers to the time origin for hypothesis testing, such as exposure, intervention, and treatment, and “the subsequence event” refers the outcome variable which contains the time-to-event concept (survival time). To avoid confusion, the terms “treatment” and “event” are used in this paper to refer to the initial event and subsequent event, respectively.
2) A clear distinction of censored data is important to preclude bias in survival analysis. Collection of data for survival analysis starts and ends at pre-determined points in time, and censored data can thus be sorted out according to the related characteristics. The most frequently encountered form of censored data is right censoring, in which the subject is alive at the end of the study period (end-of-study censoring) or the observation is terminated for reasons other than death (loss-to-follow-up censoring). Right-censored data can increase the estimated overall survival time, but may cause bias due to censoring. Left censoring concerns cases with unclear first exposure to the treatment event prior to inclusion in the study. For example, left-censored data occur if subjects are patients with a preoperative increase in plasma creatinine, because the increase in plasma creatinine can be confirmed by preoperative examination, but the onset of increase cannot be determined. Right- or left-censored data can occur depending on the follow-up interval, and all such data are called interval-censored data. For example, if the event is defined as an increase in the serum creatinine level during a postoperative period and examined at every 3 days, it may be impossible to be certain that the exact time of occurrence of the event and only know the event occurred somewhere within this interval. This is a case of right censoring, and since it occurs within the observation interval of 3 days, it is a case of intervalcensored data. Any clinical study is conducted during a predetermined follow-up period because it is impossible to continue the study until all subjects experience the event of interest. At the end of the study period, all surviving subjects are categorized as right-censored data, and this is termed “Type I censoring.”
3) If there are no censored data, the survival function S(t) can be simply expressed as “the number of patients who have not experienced the event up to a specific time (t)/the total number of patients participating in the study.” However, the probability of zero censoring being low in reality, equation 1 is typically used for survival analysis.
4) Hazard is regarded as equivalent to hazard rate in some statistics handbooks. In this paper, hazard represents hazard rate to preclude confusion.
5) These methods compare the values after assigning weights using the difference between the expected and observed counts at a given point in time. Log-rank method sets the weights at 1 at all points in time and shows the sequence-based comparison results.
6) This is the basic assumption underlying the log-rank method and the Cox proportional hazards regression model. For further details, see the explanations below.
7) The lexical meaning of hazard is something that could be dangerous as a potential cause of occurrence of the event, whereas risk refers to the probability of occurrence of the event.
8) There are multiple methods of regression diagnostics for the Cox proportional hazards regression model: checking the plot of Martingale residuals versus time, deviance residual analysis for inspecting outliers, delta-beta value analysis for checking the leverage value that may influence the model fit, Schoenfeld residual analysis for checking for timedependent changes in hazard ratio, etc.
9) The survival function s(t) is related to the hazard function h(t). The latter represents the instantaneous potential for a patient who has not yet experienced the event up a specific time (t) to experience it during the next time segment. If the hazard function does not change during the study period, i.e., h(t)= λ, the relationship between the survival and hazard functions is expressed as follows: s(t) = e−λt
10) Since the survival function is exponentially correlated with the constant λ, such a survival analysis model is termed an exponential model. For the expected value, a pilot test result or an already-known incidence rate is used.
11) The incidence rate incorporating the time factor is different in the denominator from the commonly used definition of incidence rate. For example, if one of five observed patients has experienced the event, the incidence rate is 1/5 = 0.2. This calculation omits the time factor. If the five patients are observed for two days, the incidence rate reflecting the time factor is 1/(5 × 2 days) = 0.1/person-day, and the probability of events per patient per day is 0.1. In anesthesia and pain medicine studies, it is rare to report an incidence rate estimated on the basis of the personday or person-year. Studies using the length of time as a variable, however, calculate incidence rates based on the observation period.
12) This sample size was calculated on the assumption of minimal censoring at the early study period. Given that it is unlikely that all patients are followed up throughout the observation period, an interim analysis may be necessary for adequate adjustment. Statistical power tends to decrease when the interim analysis performs, this should be compensated for by setting the sample size slightly in excess of the calculated number. For such a situation, Pocock et al. presented conservative multipliers, recommending 1.11 and 1.17 for two and three interim analyses, respectively, when the initially determined statistical power is 80%. If two interim analyses are planned in the above example case, the required number of cases determined in the study design stage is 247 × 1.11 = 274.2, i.e., 275.
Fig. 1.
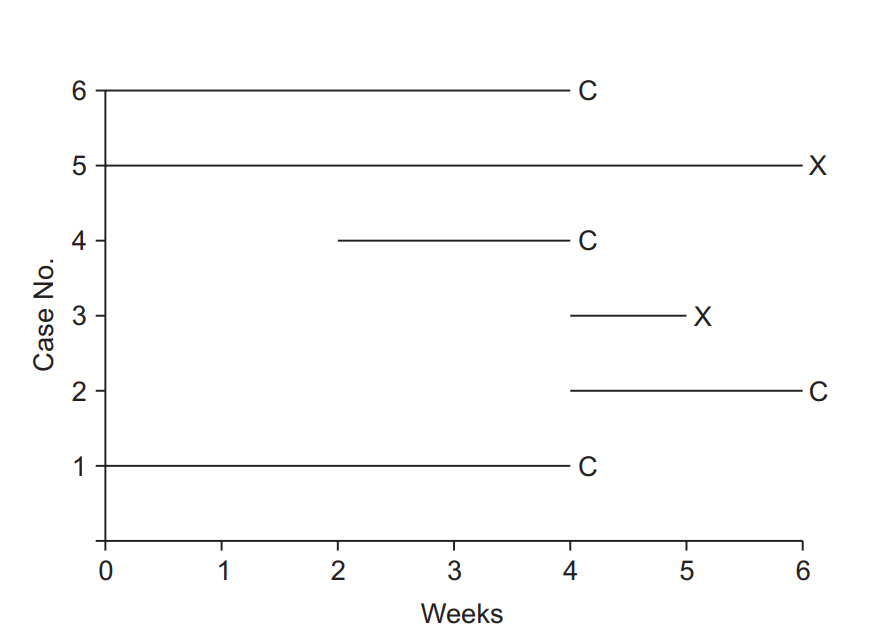
Fig. 2.

Fig. 3.
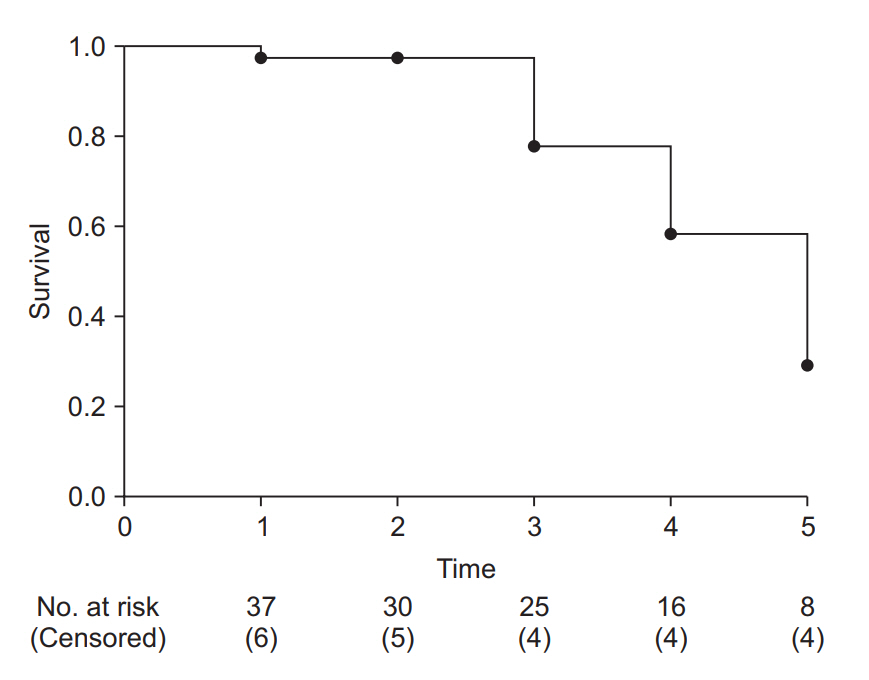
Fig. 4.

Fig. 5.
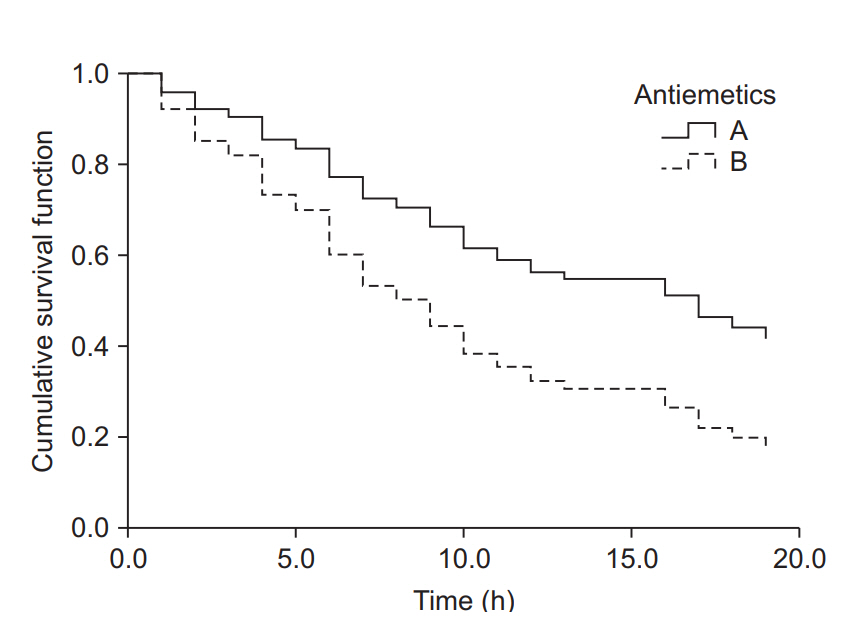
Fig. 6.
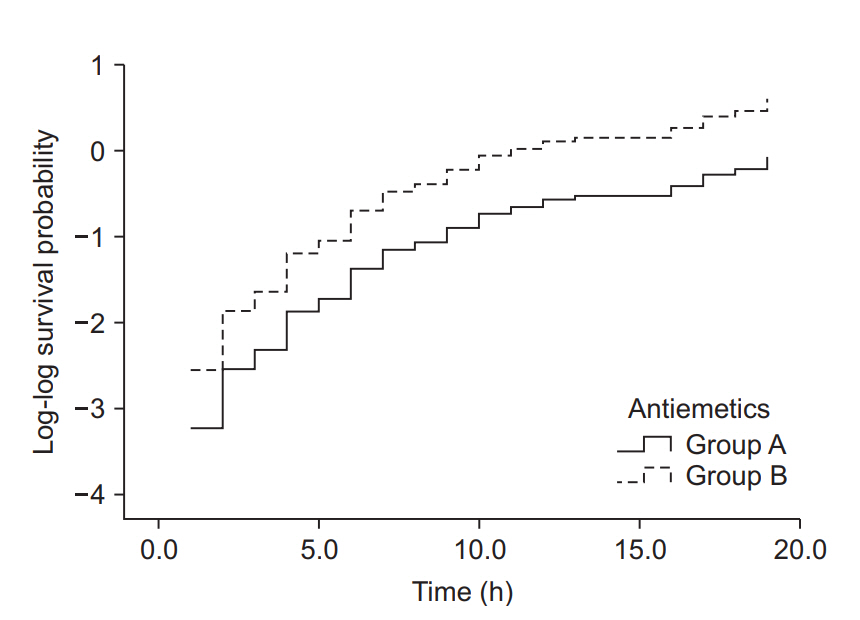
Table 1.
In this imaginary experiment, two antiemetics (A or B) were administered, and each patient was randomly allocated to a group receiving one of them. Intraoperative opioid used was recorded in the “opioid used” column. Postoperative nausea and vomiting (PONV) and its onset time were also recorded. For statistical tests such as Student’s t-test, patients 1 and 3 patients would normally be excluded (as indicated in the column labeled “Inclusion”). For survival analysis, all the patients would be included either as censored cases (numbers 1, 3, 25) or as ordinary event cases (numbers 2, 104).
Table 2.
Table 3.
| Variables | Hazard ratio | P value |
|---|---|---|
| Antiemetic | 1.95 (95% CI: 1.14–3.33) | 0.014* |
| Age | 0.99 (95% CI: 0.98–1.01) | 0.494 |
| Weight | 0.99 (95% CI: 0.97–1.02) | 0.612 |
| Opioid used | 4.87 (95% CI: 2.82–8.39) | < 0.001* |









