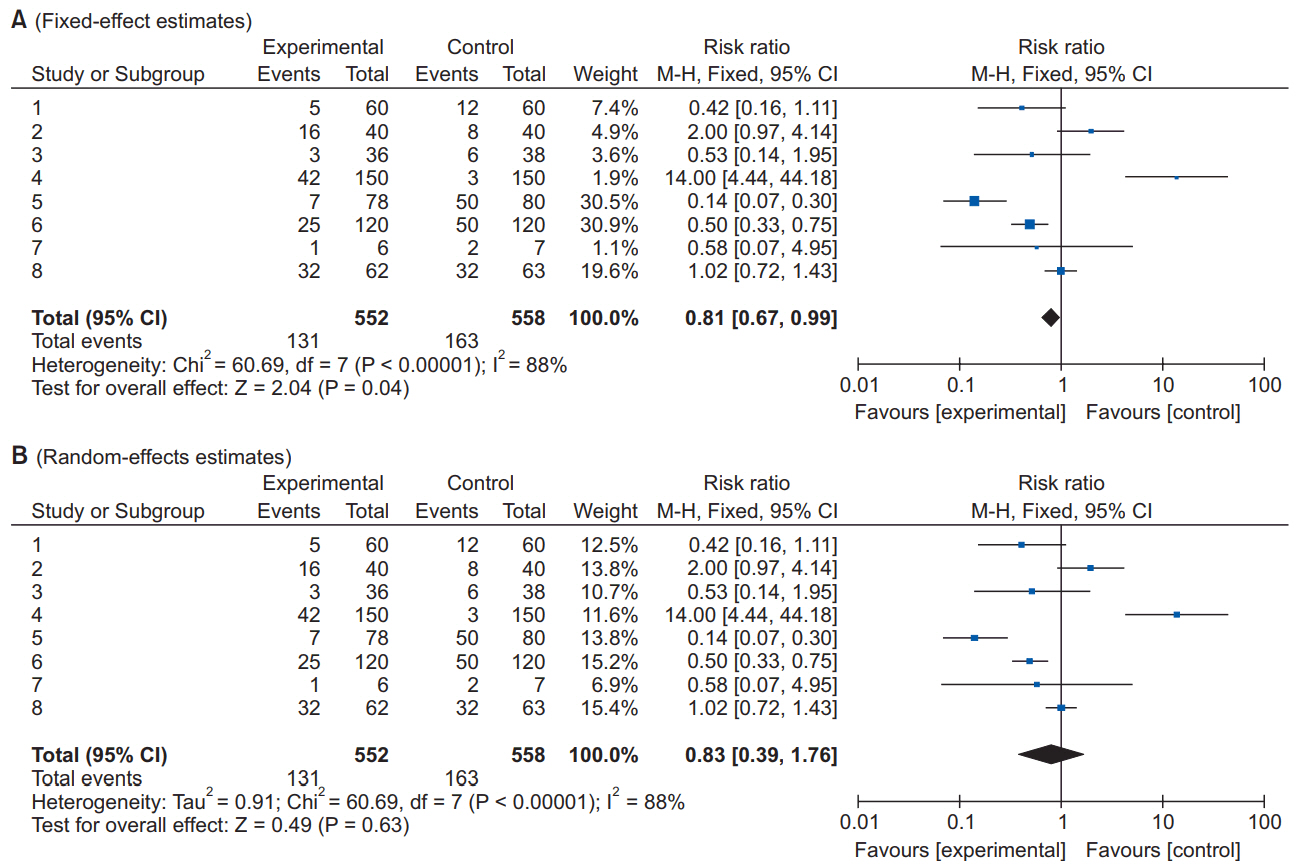
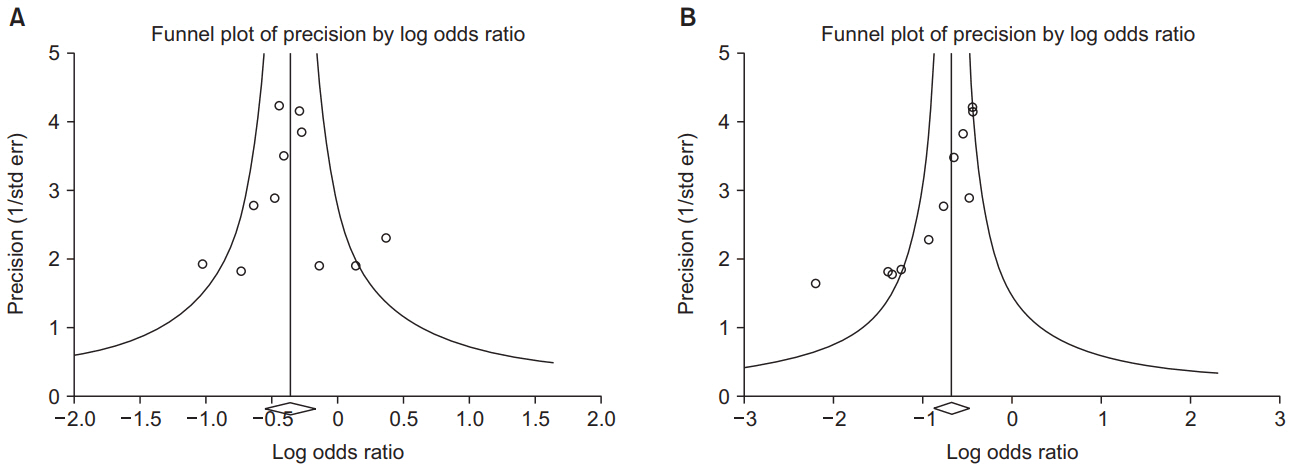
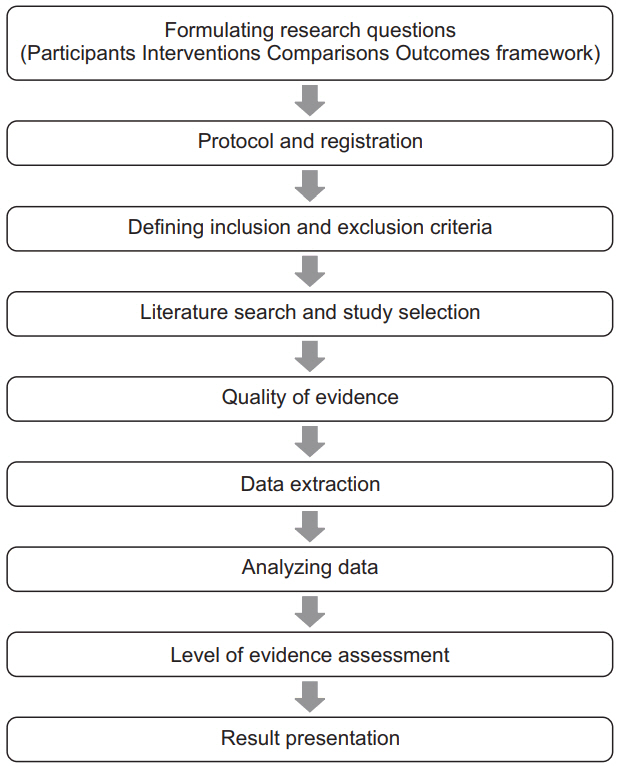
1. Kang H. Statistical considerations in meta-analysis. Hanyang Med Rev 2015; 35: 23-32.

2. Uetani K, Nakayama T, Ikai H, Yonemoto N, Moher D. Quality of reports on randomized controlled trials conducted in Japan: evaluation of adherence to the CONSORT statement. Intern Med 2009; 48: 307-13.


3. Moher D, Cook DJ, Eastwood S, Olkin I, Rennie D, Stroup DF. Improving the quality of reports of meta-analyses of randomised controlled trials: the QUOROM statement. Quality of Reporting of Meta-analyses. Lancet 1999; 354: 1896-900.


4. Liberati A, Altman DG, Tetzlaff J, Mulrow C, Gøtzsche PC, Ioannidis JP, et al. The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate health care interventions: explanation and elaboration. J Clin Epidemiol 2009; 62: e1-34.


6. Chebbout R, Heywood EG, Drake TM, Wild JR, Lee J, Wilson M, et al. A systematic review of the incidence of and risk factors for postoperative atrial fibrillation following general surgery. Anaesthesia 2018; 73: 490-8.


7. Chiang MH, Wu SC, Hsu SW, Chin JC. Bispectral Index and non-Bispectral Index anesthetic protocols on postoperative recovery outcomes. Minerva Anestesiol 2018; 84: 216-28.


10. Lam T, Nagappa M, Wong J, Singh M, Wong D, Chung F. Continuous pulse oximetry and capnography monitoring for postoperative respiratory depression and adverse events: a systematic review and meta-analysis. Anesth Analg 2017; 125: 2019-29.


11. Landoni G, Biondi-Zoccai GG, Zangrillo A, Bignami E, D'Avolio S, Marchetti C, et al. Desflurane and sevoflurane in cardiac surgery: a meta-analysis of randomized clinical trials. J Cardiothorac Vasc Anesth 2007; 21: 502-11.


12. Lee A, Ngan Kee WD, Gin T. A dose-response meta-analysis of prophylactic intravenous ephedrine for the prevention of hypotension during spinal anesthesia for elective cesarean delivery. Anesth Analg 2004; 98: 483-90.


13. Xia ZQ, Chen SQ, Yao X, Xie CB, Wen SH, Liu KX. Clinical benefits of dexmedetomidine versus propofol in adult intensive care unit patients: a meta-analysis of randomized clinical trials. J Surg Res 2013; 185: 833-43.


15. Ahn EJ, Kang H, Choi GJ, Baek CW, Jung YH, Woo YC. The effectiveness of midazolam for preventing postoperative nausea and vomiting: a systematic review and meta-analysis. Anesth Analg 2016; 122: 664-76.


17. Zorrilla-Vaca A, Healy RJ, Mirski MA. A comparison of regional versus general anesthesia for lumbarspine surgery: a meta-analysis of randomized studies. J Neurosurg Anesthesiol 2017; 29: 415-25.


18. Zuo D, Jin C, Shan M, Zhou L, Li Y. A comparison of general versus regional anesthesia for hip fracture surgery: a meta-analysis. Int J Clin Exp Med 2015; 8: 20295-301.


20. Kirkham KR, Grape S, Martin R, Albrecht E. Analgesic efficacy of local infiltration analgesia vs. femoral nerve block after anterior cruciate ligament reconstruction: a systematic review and meta-analysis. Anaesthesia 2017; 72: 1542-53.


22. Hussain N, Goldar G, Ragina N, Banfield L, Laffey JG, Abdallah FW. Suprascapular and interscalene nerve block for shoulder surgery: a systematic review and meta-analysis. Anesthesiology 2017; 127: 998-1013.


23. Wang K, Zhang HX. Liposomal bupivacaine versus interscalene nerve block for pain control after total shoulder arthroplasty: A systematic review and meta-analysis. Int J Surg 2017; 46: 61-70.


24. Stewart LA, Clarke M, Rovers M, Riley RD, Simmonds M, Stewart G, et al. Preferred reporting items for systematic review and meta-analyses of individual participant data: the PRISMA-IPD Statement. JAMA 2015; 313: 1657-65.


27. Dijkers M. Introducing GRADE: a systematic approach to rating evidence in systematic reviews and to guideline development. Knowl Translat Update 2013; 1: 1-9.
28. Higgins JP, Altman DG, Sterne JA. Chapter 8: Assessing the risk of bias in included studies. In: Cochrane Handbook for Systematic Reviews of Interventions: The Cochrane Collaboration 2011. updated 2017 Jun. cited 2017 Dec 13. Available from
http://handbook.cochrane.org.
30. Higgins JP, Altman DG, Sterne JA. Chapter 9: Assessing the risk of bias in included studies. In: Cochrane Handbook for Systematic Reviews of Interventions: The Cochrane Collaboration 2011. updated 2017 Jun. cited 2017 Dec 13. Available from
http://handbook.cochrane.org.
31. Deeks JJ, Altman DG, Bradburn MJ. Statistical methods for examining heterogeneity and combining results from several studies in meta-analysis. In: Systematic Reviews in Health Care. Edited by Egger M, Smith GD, Altman DG: London, BMJ Publishing Group. 2008, pp 285-312.
34. Thompson SG. Controversies in meta-analysis: the case of the trials of serum cholesterol reduction. Stat Methods Med Res 1993; 2: 173-92.


36. Sutton AJ, Abrams KR, Jones DR. An illustrated guide to the methods of meta-analysis. J Eval Clin Pract 2001; 7: 135-48.


37. Begg CB, Mazumdar M. Operating characteristics of a rank correlation test for publication bias. Biometrics 1994; 50: 1088-101.


38. Duval S, Tweedie R. Trim and fill: a simple funnel-plot-based method of testing and adjusting for publication bias in meta-analysis. Biometrics 2000; 56: 455-63.