|
 |
| Korean J Anesthesiol > Volume 73(4); 2020 > Article |
|
Abstract
Intergroup comparability is of paramount importance in clinical research since it is impossible to draw conclusions on a treatment if populations with different characteristics are compared. While an adequate randomization process in randomized controlled trials (RCTs) ensures a balanced distribution of subjects between groups, the distribution in observational prospective and retrospective studies may be influenced by many confounders.
Propensity score (PS) is a statistical technique that was developed more than 30 years ago with the purpose of estimating the probability to be assigned to a group. Once evaluated, the PS could be used to adjust and balance the groups using different methods such as matching, stratification, covariate adjustment, and weighting. The validity of PS is strictly related to the confounders used in the model, and confounders that are either not identified or not available will produce biases in the results. RCTs will therefore continue to provide the highest quality of evidence, but PS allows fine adjustments on otherwise unbalanced groups, which will increase the strength and quality of observational studies.
In clinical research, conclusions on treatments are derived from the comparison of groups. Validity of this comparison is granted by homogeneity between groups, and populations with different baseline characteristics can potentially lead to biased results that are of poor quality.
Randomized controlled trials (RCTs) provide the highest quality of evidence; when adequately powered, and after effective randomization, selection and other types of bias are reduced [1], and each group will have the same baseline characteristics resulting in optimal intergroup comparability. Despite their advantages, RCTs are not always feasible because of their cost, length, ethical issues, or all of the above. Furthermore, if randomization is not performed properly it might underpower the study or lead to the patients being allocated to the incorrect treatment groups [2]. In these cases, well-designed prospective or retrospective observational studies may be used to compare groups and estimate the effectiveness of treatments. However, a poor balance among compared groups remains a significant issue when measuring the quality of evidence provided by such studies.
Consider applying two different treatments (let them be respectively laryngeal mask A: LMAa and laryngeal mask B: LMAb) to a subject: the observed dichotomous outcome could only be one (sore throat present or absent).
Called E the measured effect, we can describe the average treatment effect as:
E=E(LMAa)- E(LMAb)
However, we have to consider that the measured effect (sore throat) could be biased by many confounders resulting from an unbalanced subject allocation between groups; in our example, to simplify, let them be: surgical time, body mass index (BMI), and age. All the confounders could be summed into a vector (xi), and the groups can be compared when the conditional distribution of x, given the balancing function b(x), is the same for both the LMAa and LMAb groups. When properly performed, randomization distributes the confounders equally among groups.
Translated into our example, LMAa may be preferred by some anesthesiologists because of their personal experience, as a result of local protocols for longer surgeries, in patients with an elevated BMI, or in older patients. Indeed, LMAa may be beneficial in reducing sore throat complications (Chi-square test, P < 0.001). However, it is not possible to know if this is directly caused by LMAa or whether it is biased by the BMI and the surgery length differences in the group (Table 1). Propensity score (PS) methods are matching models used to reduce or minimize the effect of confounders (e.g., selection bias) whenever non-randomized prospective or retrospective datasets are analyzed.
The objective of this statistical round is to provide a definition of PS, evaluate PS adequacy, briefly describe the PS adjustment methods themselves, and to discuss the limitations of such methods. To exemplify, we will continue the hypothetical retrospective study evaluating the new laryngeal mask A compared to another laryngeal mask B over sore throat development. All statistical analyses were conducted using R version 3.4.0 (2017-04-21) and the MatchIt package [3]. P < 0.05 were considered statistically significant.
The dataset discussed and the R script used in this manuscript are fully available as supplementary material (Supplementary Material 1, Sheet 1 and Supplementary Material 2, respectively).
PS is the estimated probability for each individual enrolled in a study to be assigned to one of the groups of comparison after taking into account all the predetermined confounders [4], and can be formally expressed as:
PS = P(Xi) = Probability (Treatment = 1|Xi).
It represents the probability of a patient (i), being exposed to influencing confounders (Xi), to be assigned to Treatment (dichotomous research variable of interest, in our case LMAa = 1, LMAb = 0).
Therefore, the aim of a PS analysis is to eliminate the differences among compared groups for predefined variables (predetermined confounders) by matching the individuals of a population with the individuals of the other population.
Since PS is a probability, it ranges from 0 to 1. If we conduct a RCT to solve the question of our aforementioned example, to assess sore throat development after using LMAa and LMAb, and if we use an adequate randomization method, each member of our study will have a PS of 0.5, having the same probability to be assigned to either the LMAa or the LMAb group. In our non-randomized observational example, PS will vary for each subject, fluctuating between 0 and 1, since the chances of being allocated to one group are not completely random (PS 0.5) as stated above.
The most common way to calculate PS is logistic regression. However, other techniques have been proposed such as bagging or boosting, recursive partitioning, or tree-based methods and random forests [5,6].
Table 2 shows an example of the logistic regression method applied to our example.
PS analysis relies on the following assumptions:
a) The ignorable treatment assignment assumption
After taking into account all confounders, the assignments to treatment conditions are independent from the treatment effect. In order to achieve this assumption, all the variables that could possibly lead to bias should be incorporated in our model to prevent the biased allocation of a subject to a group.
b) The stable unit treatment value assumption
The observation of one subject should be unaffected by the particular assignment of treatment to the other subjects [7]: this means that the outcome is not related to the assignment procedure and that all participants receiving a specific treatment should actually receive the same treatment [4].
c) Sufficient overlap
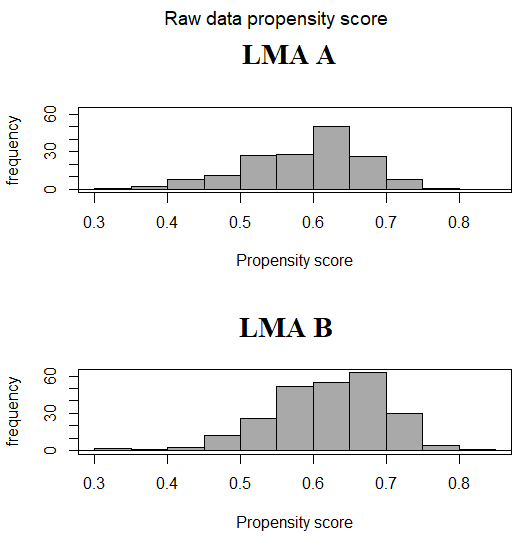
The distribution of PS between groups should have sufficient overlap in order to properly match the subjects. The comparison can be made in several ways such as visual inspection of the graph of PS distribution [8], comparison of the minimum and the maximum value of PS for each group [9], or evaluation by inferential test or by mean difference if the PS are significantly different [10]. Fig. 1 shows the histogram of the distribution of the calculated PS between the two populations of our example showing an adequate overlap.
We report in the supplementary material the estimated PS in our sample (Supplementary material 1, Sheet 2).
Once evaluated, the PS can be used to balance the groups using different adjustment methods such as matching, stratification, covariate adjustment (or regression), and weighting.
PS matching means that every subject in a group is matched to a subject in the other group with an identical or similar PS in a 1 : 1 ratio. Several different methods can be used to accomplish the matching procedure.
A subject in the treatment group is matched to a subject in the control group with the same PS. If this is not possible, the subjects are excluded from the analysis.
A subject in the treatment group is matched with the subject in the control group with the closest PS. This method guarantees that every subject in the treatment group is assigned to a subject in the control group. If two subjects are equally distant, then the selection is random. However, it is possible that inappropriate matches are formed between subjects with an elevated difference in PS.
It is possible to decide the threshold to the acceptable closest PS by specifying a caliper distance, that is, the maximum acceptable distance in PS to form a match. Then, subjects with a PS difference higher that the selected caliper are not available. It follows that not all subjects in the treatment group may find a match. Although the acceptable ‘similar PS’ is not absolute (various thresholds can be found in medical literature), it has been suggested that using a caliper width of 0.2 standard deviations of the logit of the PS is adequate. Nonetheless, when all of the covariates are binary, the choice of caliper width has a much smaller impact [11,12]
A greedy matching is a matching procedure where the first subject of the treatment group is selected randomly and assigned to the corresponding subject in the control group to form a match, then another subject is selected in the treatment group to form a match, and the process continues until all the subjects in the treatment group are assigned or there are no more possible matches. It is called greedy because this method establishes the match without considering if the subject in the control group could be matched to a more suitable subject in the treatment group.
In contrast to greedy matching, optimal matching works in order to minimize the total PS within-pair difference. However, optimal matching is not superior to greedy matching in producing balanced matched samples [13].
Once matched, the subject in the control group can be removed from the pool of the matchable subjects (matching without replacement) or may be used for further matching (matching with replacement). The latter leaves a subject in the control group that is possibly matched to more than one subject in the treatment group [12,14].
As stated above, the most common PS matching strategies use a one-to-one matching whereby each subject in the treatment group is assigned to a subject in the control group; this is the a logical way to proceed when the size of the two groups is similar. However, considering a situation where we have n subjects in the treatment group and ten times n subjects in the control group. Matching one-to-one would mean losing nine times n subjects of the control group because they will not be matched. Many-to-one matching means that a predetermined number of subjects in the control group is assigned to one subject in the treatment group (three to one, four to one and so on) avoiding loss of information. Nonetheless, increasing the number of control subjects matched to each treated subject leads to an increased bias in estimating the treatment effects [15].
Once the pairs are formed, all the subjects not included in the pairs are eliminated and the treatment effect can be calculated using a paired t-test on a continuous outcome and a McNemar's for a dichotomous outcome [11].
The stratification technique divides subjects into homogeneous groups based on their PS, and it has been demonstrated that by using at least five groups the likelihood of bias may be reduced by up to 90% [16]; there is no maximum number of groups, and it should be noted that quintiles are normally used. Although increasing the number of subgroups may reduce bias, the relative reduction of the bias might decrease at each subgroup increase [16–18]. Once the subgroups have been identified, the treatment effect can be calculated for each stratum, weighting the effect on the subject size of each subgroup, and eventually it can be summed in an overall treatment effect.
Covariate adjustment using the PS implies the use of a further multivariable regression analysis following the PS calculation. The outcome variable is used as the dependent variable, while PS serves as the predictor variable. If the outcome variable is dichotomous, a logistic regression may be used, whereas if the outcome variable is continuous, a linear model should be chosen; in the first case, the effect of the treatment will be the adjusted odds ratio, whereas in the second case, the effect will be the adjusted difference in means.
Weighting, or more properly inverse probability of treatment weighting, is the fourth and last method that will be discussed. Initially proposed in 1987 [19], this method is based on assigning a weight to every member of the population.
The weight of a treated subject is defined as the inverse of its PS:
w(LMAa) = 1/PS
The weight of a control subject is defined as the inverse of one minus its PS:
w(LMAb) = 1/(1-PS)
This permits the creation of a new population derived from a subgroup of the initial population, ideally not influenced by the identified confounders, leading to an unbiased estimate of the treatment effect.
In our example, we chose to match the population with the nearest neighbor method (0.1 caliber), resulting in 324 subjects (162 per group) (Supplementary material 1, Sheet 3); Table 3 depicts the comparison between confounders in the two new populations.
Sore throat still results significantly different between groups (P < 0.001) but through the PS adjustment of our analysis and with added strength to our conclusion.
In order to have a complete overview of PS methods it is mandatory to acknowledge their limitations. First, the validity of PS methods is strictly related to the confounders integrated in the model, and not identified or not available confounders will continue to produce biases in our results. In a prospective observational study, we may not be aware of some specific variables, whereas in a retrospective study, the variable may be simply missed in the database, resulting in both cases in altered group allocation and therefore invalidity of the results. Therefore, a thorough clinical knowledge is mandatory to minimize umbalacement when operating with PS.
Secondly, clinicians should not include model variables that are consequences of the exposure, which may lead to an ‘over-adjusted’ model and biased effect estimates. Indeed, if multiple predictors of exposure that are not causally associated with the outcome are included, the power is unnecessarily lowered. Thirdly, the quality of matches can be an issue when the number of subjects in the control group is limited or when the treatment and control groups present with differences. If matching causes an imbalance among the population, the clinician should consider a different matching method, for example using replacement [20].
While RCTs remain the gold standard for quality of evidence (especially after an optimal randomization) and should be performed whenever possible, PS adjustment is a powerful method to increase the strength of observational studies if a thorough analysis of its limits and potential biases is performed in parallel.
NOTES
Author Contributions
Alessandro De Cassai (Conceptualization; Supervision; Writing – original draft; Writing – review & editing)
Giulio Andreatta (Conceptualization; Writing – original draft; Writing – review & editing)
Annalisa Boscolo (Writing – original draft; Writing – review & editing)
Marina Munari (Supervision; Writing – review & editing)
Paolo Navalesi (Supervision; Writing – review & editing)
Table 1.
Univariate Analysis of Confounders and Sore Throat among LMAa and LMAb Groups
Table 2.
Logistic Regression Analyses
Table 3.
Clinical Characteristics of the Total and Matched Populations among LMAa and LMAb Groups
References
3. Ho D, Imai K, King G, Stuart E. MatchIt: Nonparametric preprocessing for parametric causal inference. J Stat Soft 2011; 42: 1-28.

4. Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika 1983; 70: 41-55.

5. Lee BK, Lessler J, Stuart EA. Improving propensity score weighting using machine learning. Stat in Med 2010; 29: 337-46.

6. McCaffrey DF, Ridgeway G, Morral AR. Propensity score estimation with boosted regression for evaluating causal effects in observational studies. Psychol Methods 2004; 9: 403-25.


7. Cox DR. The regression analysis of binary sequences. J R Stat Soc: Series B Stat (Method) 1958; 20: 215-32.

9. Caliendo M, Kopeinig S. Some practical guidance for the implementation of propensity score. J Econ Surv 2008; 22: 31-72.

10. Diamond A, Sekhon JS. Genetic matching for estimating causal effects: a general multivariate matching method for achieving balance in observational studies. The Rev Econ Stat 2013; 95: 932-45.

11. Austin PC. An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivariate Behav Res 2011; 46: 399-424.



12. Austin PC. Propensity-score matching in the cardiovascular surgery literature from 2004 to 2006: a systematic review and suggestions for improvement. J Thorac Cardiovasc Surg 2007; 134: 1128-35.


13. Austin PC. A critical appraisal of propensity score matching in the medical literature from 1996 to 2003. Stat Med 2008; 27: 2037-49.


14. Gu XS, Rosenbaum PR. Comparison of multivariate matching methods: structures, distances, and algorithms. J Comput Graph Stat 1993; 2: 405-20.

15. Austin PC. Statistical criteria for selecting the optimal number of untreated subjects matched to each treated subject when using many-to-one matching on the propensity score. Am J Epidemiol 2010; 172: 1092-7.



16. Cochran WG. The effectiveness of adjustment by subclassification in removing bias in observational studies. Biometrics 1968; 24: 295-313.