Survival analysis: part II – applied clinical data analysis
Article information
Abstract
As a follow-up to a previous article, this review provides several in-depth concepts regarding a survival analysis. Also, several codes for specific survival analysis are listed to enhance the understanding of such an analysis and to provide an applicable survival analysis method. A proportional hazard assumption is an important concept in survival analysis. Validation of this assumption is crucial for survival analysis. For this purpose, a graphical analysis method and a goodnessof- fit test are introduced along with detailed codes and examples. In the case of a violated proportional hazard assumption, the extended models of a Cox regression are required. Simplified concepts of a stratified Cox proportional hazard model and time-dependent Cox regression are also described. The source code for an actual analysis using an available statistical package with a detailed interpretation of the results can enable the realization of survival analysis with personal data. To enhance the statistical power of survival analysis, an evaluation of the basic assumptions and the interaction between variables and time is important. In doing so, survival analysis can provide reliable scientific results with a high level of confidence.
Introduction
The previous article ‘Survival analysis: Part I – analysis of time-to-event’ introduced the basic concepts of a survival analysis [1]. To decrease the gap between the data from a clinical case and a statistical analysis, this article presents several extended forms of the Cox proportional hazards (CPH) model in-series.
The most important aspect of the CPH model is a proportional hazard assumption during the observation period. The hazard of an event occurring during an observation cannot always be remained constantly, and the hazard ratio cannot be maintained at a constant level. This is the main obstacle for a clinical data analysis using a CPH model.
The basic concepts required to understand and interpret the results of a survival analysis were covered in a previous article [1]. Part 2 of this article, described herein, focuses on the analytical methods applying clinical data and coping with problems that can occur during an analysis. Such methods for validating a proportional hazard assumption apply clinical data and several extended Cox models to overcome the problem of a violated proportional hazard assumption. This article also includes the R codes used for estimating several Cox models based on clinical data. For those familiar with a statistical analysis, the R codes can easily enable an extension of the Cox model estimation.1)
Proportional Hazard Assumption
Refer to the previous article [1] for a description of diagnostic methods applied to a CPH model. Here, we consider only a proportional hazard assumption. A hazard is defined as the probability of an event occurring at a time point (t). The survival function of a CPH model is an exponential function, and the hazard ratio (λ) is constant during an observation; thus, a survival function is defined in the exponential form of the hazard ratio at a time point (equation 1) [1].
To estimate hazard ratio, which is included in the survival function, hazard function (h) is required and it contains a specific explanatory variable (X) which indicates a specific treatment or exposure to a specific circumstance. At the time point of t, the hazard function of the control group is defined as the basal hazard function (h0 (t)), and hazard function of the treatment group as the combined form of the basal hazard function and a certain function with the explanatory variable (X). The hazard ratio is the value of the hazard functions of treatment over control groups (equation 2) [2].
As shown in equation 2, the CPH model processes the analysis under the constant hazard ratio assumption with the explanatory variable, which is not affected by the time [3]. The hazard ratio remains constant, and the hazards of each group at any time point remain at a distance and never meet graphically during an observation. However, this does not guarantee the satisfaction of the proportional hazard assumption. In a clinical setting, one hazard could remain lower or higher than the others, and their ratio cannot be constant because the treatment effect may vary owing to various factors. Therefore, we need a statistical method to prove the satisfaction or violation of the proportional hazard assumption.
Validation of Proportional Hazard Assumption
There are three representative validation methods of a proportional hazard assumption. One is a graphical approach, another is using the goodness of fit (GOF), and the last is applying a time-dependent covariate [4,5].
Graphical analysis for validation of proportional hazard assumption
As mentioned in the previous article, a log minus log plot (LML plot) is one of the most frequently used methods for the validation of a proportional hazard assumption [1]. The log transformation is applied twice during a mathematical process for estimating the survival function. The first log transformation results in negative values because the probability values from the survival function lay between zero and 1, and such values should be made positive to conduct a second log transformation. The name of the LML plot implies this process. A survival function is the exponential form of a hazard ratio, and the hazard ratio is constituted with the hazard function, which is an exponential form of an explanatory variable. As a result of an LML transformation, the survival function is converted into a linear functional form, and the difference from the explanatory variable creates a distance on the y-axis at a time point. Ultimately, survival functions that are log transformed twice become parallel during the observation period. Deductively, two curves on an LML plot also become parallel, which indicates that the hazard ratio remains constant during the observation period [4].
There is a risk of subjective decision regarding the validation of a proportional hazard assumption using an LML plot because this method is based on a visual check. It is recommended that the interpretation be as conservative as possible except under strong evidence of a violation, including instances in which the curves are crossing each other or apparently meet. A continuous explanatory variable should be converted into a categorical variable of two or three levels to produce an LML plot. When doing so, the data thin out and a different result can be reached according to the criteria used for dividing the variable [5].
R codes for Kaplan–Meier survival analysis under the assumption of a proportional hazard
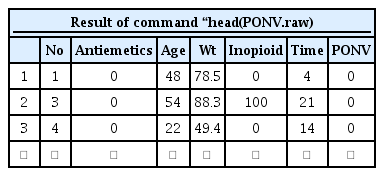
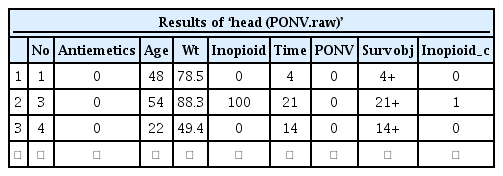
The sample data ‘Survival2_PONV.csv’ contains the imaginary data of 104 patients regarding the first onset time of postoperative nausea and vomiting (PONV). All patients received one of two types of antiemetics (Drugs A or B). The columns represent the patient number (No), types of antiemetics (Antiemetics), age (Age), body weight (Wt), amount of opioid used during anesthesia (Inopioid), the first PONV onset time (Time), and whether PONV occurred (PONV). To load such data into R software 3.5.2 (R Development Core Team, Vienna, Austria, 2018), the following code can be used. In this code, the location of the CSV file on the hard drive is ‘d:’, and users should adequately modify the path. This code provides the first several lines of data (Table 1).
# Read data
PONV.raw <- read.csv ("d:/Survival2_PONV.csv",
TRUE, sep = ","
)
# Check imported data
head(PONV.raw)
To conduct a survival analysis using R, two R packages are required, ‘survival’2), and ‘survminer’.3) When these packages are not supplied as a default, manual installation is not difficult when using the command ‘install.packages(“package name”)’. These packages are then called.
#Load Package: survival, survminer
library (survival)
library (survminer)
Then, a Kaplan–Meier survival analysis is applied. The following code covers a Kaplan–Meier analysis, comparing the PONV using a log-rank test, and the LML plot introduced in part I of this article [1]. Small modifications of this code can enable a survival analysis with the user’s own data.
### Kaplan-Meier Estimation (KME)
#Add survival object
PONV.raw$Survobj <- with(PONV.raw,
Surv(Time, PONV == 1)
)
head (PONV.raw)
## Single KME. The log-log confidence interval is preferred.
km.one <- survfit(Survobj ~1, data = PONV.raw,
conf.type = "log-log")
# Result of KME
km.one
# Survival table
summary (km.one)
# Survival curve
ggsurvplot (km.one, data = PONV.raw,
conf.int = TRUE,
palette = "grey",
surv.median.line = "hv",
break.time.by = 4,
censor = TRUE,
legend = "none",
xlab = "Time (hour)",
risk.table = TRUE,
tables.height = 0.2,
tables.theme = theme_cleantable(),
risk.table.y.text = FALSE
)
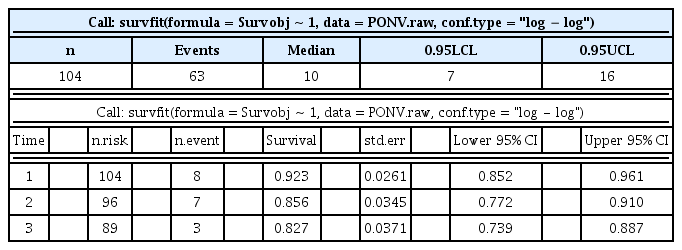
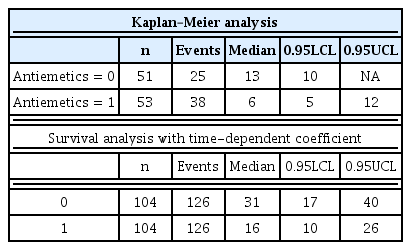
R applies a Kaplan–Meier analysis using the new variable ‘Survobj’. The results of a Kaplan–Meier analysis and a survival table are presented in Table 2. Out of 104 patients, 63 patients suffered from PONV, and the median onset time was 10 h. A graphical presentation is also possible (Fig. 1). Here, ‘ggsurvplot’ produces survival curves with complex arguments, fine-tuning the argument options to draw intuitive graphs.
Kaplan–Meier curve of overall survival status with sample data. A 95% confidence interval (estimated from a log hazard) is presented in the shadowed area. The dashed line indicates the median survival time.
The next code is for an estimation of the survival curves according to two antiemetics and conducting a log-rank test.
### KME by Antiemetics
km.antiemetics <- survfit (Survobj ~ Antiemetics,
data = PONV.raw,
conf.type = "log-log"
)
# Result of KME by Antiemetics
km.antiemetics
# Survival table of KME by Antiemetics
summary (km.antiemetics)
# KM estimation, log-rank test
survdiff ( formula = Surv(Time, PONV == 1)
~ Antiemetics,
data = PONV.raw
)
# Survival curve of KME by Antiemetics
ggsurvplot ( km.antiemetics, data = PONV.raw,
fun = "pct", pval = TRUE,
conf.int = TRUE, surv.median.line = "hv",
linetype = "strata", palette = "grey",
xlab="Time (hour)",
legend.title = "Antiemetics",
legend.labs = c("Drug A", "Drug B"),
legend = c(.1, .2), break.time.by = 4,
risk.table = TRUE,
tables.height = 0.2,
tables.theme = theme_cleantable(),
risk.table.y.text.col = TRUE,
risk.table.y.text = TRUE
)
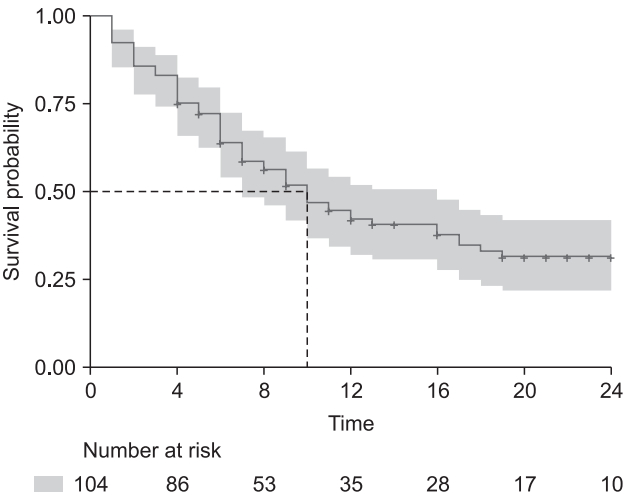
Table 3 and Fig. 2 show the results of this code. Antiemetics are coded as 0 for Drug A and 1 for Drug B, namely ‘Antiemetics = 0’ and ‘1’ represent Drugs A and B, respectively in the Table and Figure.
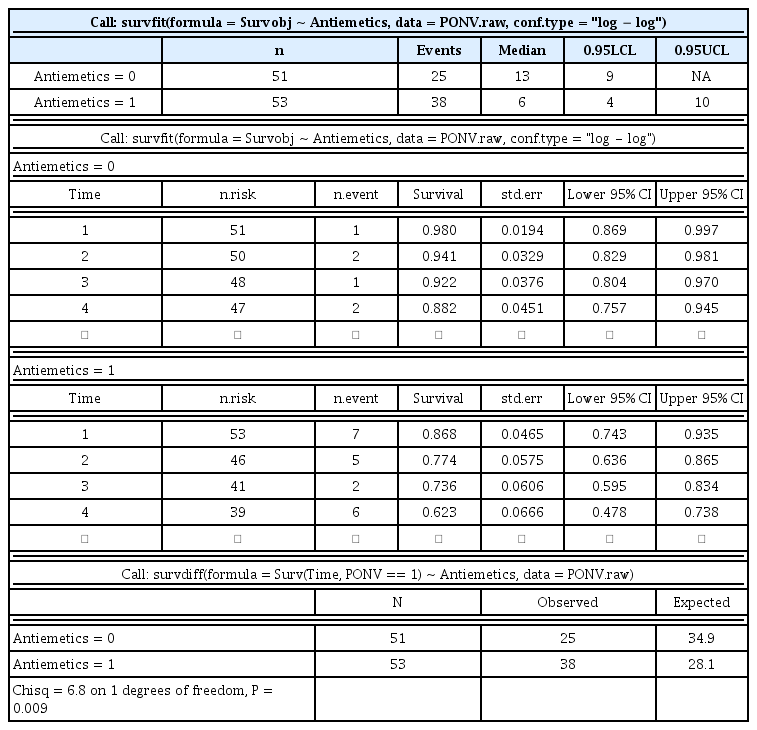
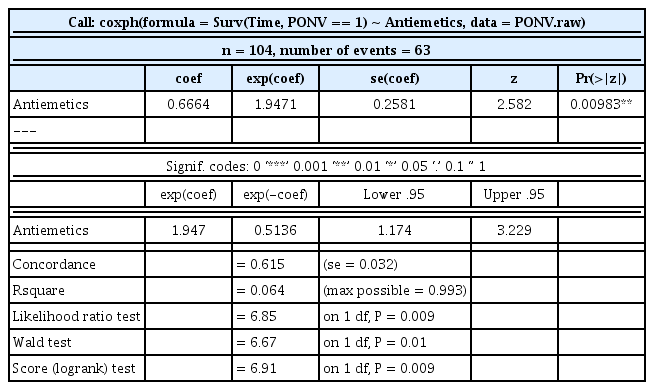
Results of Kaplan–Meier Estimation between Antiemetics, Survival Tables of Two Antiemetics, and Comparison Results of Log-rank Test
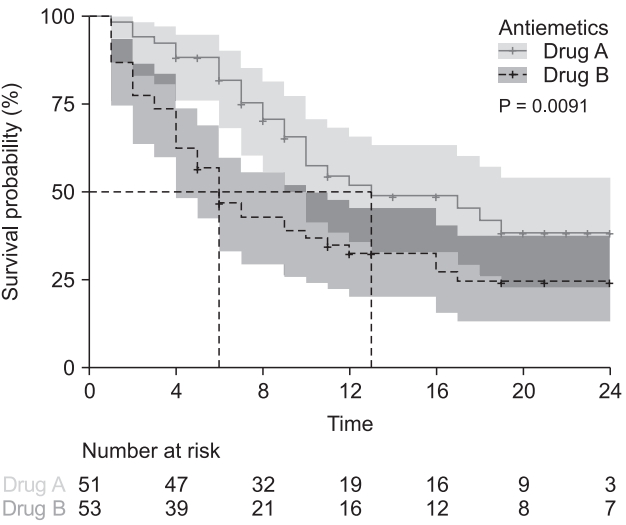
Kaplan–Meier curves of two antiemetics with sample data. The P value is estimated based on a log-rank test. A 95% confidence interval (estimated from a log hazard) is presented in the shadowed area. The dashed lines indicate the median survival times of groups taking Drugs A and B. Drug A is coded as ‘Antiemetics = 0’ and Drug B is coded as ‘Antiemetics = 1’ in the original data.
As the interpretation of a log-rank test, the survival functions of two antiemetics are statistically different (P = 0.009), and the median PONV free time is 13 and 6 h for Drugs A and B, respectively.
The log-rank test is also based on the proportional hazard assumption, and an LML plot can be used to validate this assumption. The code for this process is as follows, and the output graph is shown in Fig. 3.4,,5)

Log minus log plot of Kaplan–Meier estimation with log-rank test between two antiemetics. The two curves do not meet during the observation period, indicating the satisfaction of the proportional hazard assumption. The log-time scale is shown in the x-axis.
# LML plot
plot (survfit(Surv(Time, PONV == 1) ~ Antiemetics,
data = PONV.raw), fun = "cloglog")
The goodness of fir test (GOF test)
The second method for validating a proportional hazard assumption is a GOF test between the observed and estimated survival function values. This provides a P value and hence is a more objective method than a visual check [5].
A Schoenfeld residual test is a representative GOF test for validation of a proportional hazard assumption [6–8]. A Schoenfeld residual is the difference between explanatory variables observed in the real world and estimated using a CPH model for patients who experience an event. Thus, Schoenfeld residuals are calculated using all explanatory variables included in the model. If the CPH model includes two explanatory variables, the two Schoenfeld residuals come out for one patient at a time.6)
Because the hazard ratio is constant during the observation period (a proportional hazard assumption), Schoenfeld residuals are independent of time. A violation of the proportional hazard assumption may be suspected when the Schoenfeld residual plot presents a relationship with time. Also, a Schoenfeld residual test is possible under a null hypothesis of ‘there is no correlation between the Schoenfeld residuals and ranked event time’.7)
Schoenfeld residual tests cannot be used to validate a proportional hazard assumption in a Kaplan–Meier estimation because it is based on estimated values using the CPH model. A Schoenfeld residual test is lacking in terms of the statistical hypothesis testing process. Null hypothesis significance testing applies a statistical process to validate ‘no difference,’ and when the null hypothesis is not true under a significant level, an alternative hypothesis is true except for the probability of the significance level, that is, differences exist between comparatives within the probability of significance. A Schoenfeld residual test determines whether a proportional hazard assumption is violated based on the probability of the correlation statistics. Correlation statistics with a higher probability than the significance level result in a satisfaction of the proportional hazard assumption without null hypothesis testing. This method cannot guarantee sufficient evidence to reject a hypothesis, however. Furthermore, the P value is dependent on the sample size, and large sample size will produce a high significance with a minimal violation of the assumption; an apparent assumption violation may be insignificant with small sample size. Although a Schoenfeld residual test is more objective than an LML plot, the use of two methods simultaneously is recommended owing to the problems listed above [4,5,7].
R codes for the Cox proportional hazard regression model and GOF test
To estimate a CPH model, libraries used in a Kaplan–Meier analysis are also required. After importing the data and calling the required libraries, the CPH model can be estimated according to the antiemetics using the following code.
# Univariate Cox proportional hazard model
# for a single covariate
cph.antiemetics <- coxph(Surv(Time, PONV == 1) ~ Antiemetics
, data = PONV.raw
)
summary(cph.antiemetics)
Table 4 summarizes the results. The PONV incidence rate is 1.9471-fold higher (95% CI, 1.174–3.229, P = 0.010) in the drug B groups than in the drug A groups.
Survival2_PONV.csv has four covariates. A multivariate analysis is possible using these covariates with a CPH model. Multivariate analysis can estimate the most compatible model, including significant covariates, through regression diagnostic statistics. Still, several controversies remain [9], both directional stepwise selection methods are applied in this example.
# Multivariate Cox regression
cph.full <- coxph (Surv(Time, PONV == 1)
~ Antiemetics + Age + Wt + Inopioid
, data = PONV.raw
)
summary (cph.full)
# Variables selection
cph.selection <- step(
coxph(Surv(Time, PONV == 1)
~ Antiemetics + Age + Wt + Inopioid
, data = PONV.raw)
, direction = "both"
)
summary (cph.selection)
# Final model selected
cph.selected <- coxph(Surv(Time, PONV == 1)
~ Antiemetics + Inopioid
, data = PONV.raw
)
summary (cph.selected)
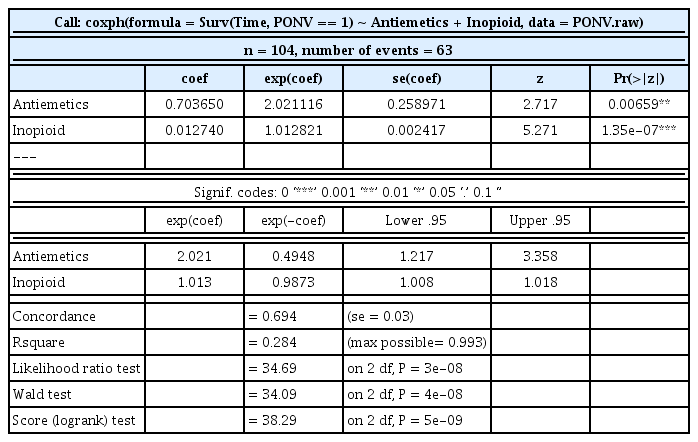
After examining the full model including all covariates (summary(cph.full)), the most compatible model is confirmed through a covariate selection (summary(cph.selection)), and a clean result is finally obtained (summary(cph.selected)). Table 5 shows the final model. According to the result, the PONV increment is estimated as 2.021-fold (95% CI, 1.217–3.358, P = 0.007) based on the antiemetics, and 1.013-fold (95% CI, 1.008–1.018, P < 0.001) based on intraoperative opioid usage.
The next code draws survival curves against the antiemetics for the final model (Fig. 4).8)

Survival curves of antiemetics estimated using the Cox proportional hazards regression model. a solid black line indicates Drug A (Antiemetics = 0) and a solid grey line indicates Drug B (Antiemetic = 1). Dashed lines present a 95% CI range. Drug A is coded as ‘Antiemetics = 0’ and drug B is coded as ‘Antiemetics = 1’ in the original data.
# Survival curves of the Cox PH model
# grouped by Antiemetics
new.cph.antiemetics <-with (PONV.raw
,data.frame(Antiemetics = c(0, 1),
Inopioid = c(0,0)
))
new.cph.antiemetics.fit <- survfit(cph.selected
, newdata = new.cph.antiemetics
)
ggsurvplot(new.cph.antiemetics.fit
, data = PONV.raw
, conf.int = TRUE
, conf.int.style = "step"
, censor = FALSE
, palette = "grey"
, break.time.by = 4
, linetype = "solid"
, axes.offset = FALSE
, xlab = "Time (hour)"
, legend = c(0.1, 0.15)
, legend.labs = c("Drug A", "Drug B")
, legend.title = "Antiemetics")
The R code for an LML plot is described above. For categorical variables, an LML plot provides an easy to interpret and intuitive validation method for a proportional hazard assumption.9,) Validation of the proportional hazard assumption of the antiemetics, which is a categorical variable, is possible using an LML plot. (Fig. 5)
#LML for CoxPH
plot (survfit(coxph(Surv(Time, PONV == 1)
~ strata(Antiemetics)
, data = PONV.raw
)
),
fun = "cloglog"
)
The proportional hazard assumption of the antiemetics is not violated according to the graphs shown in Fig. 5. The covariate “Inopioid” is a continuous type of variable, and an LML plot using this variable is impossible to achieve without a categorical transformation.
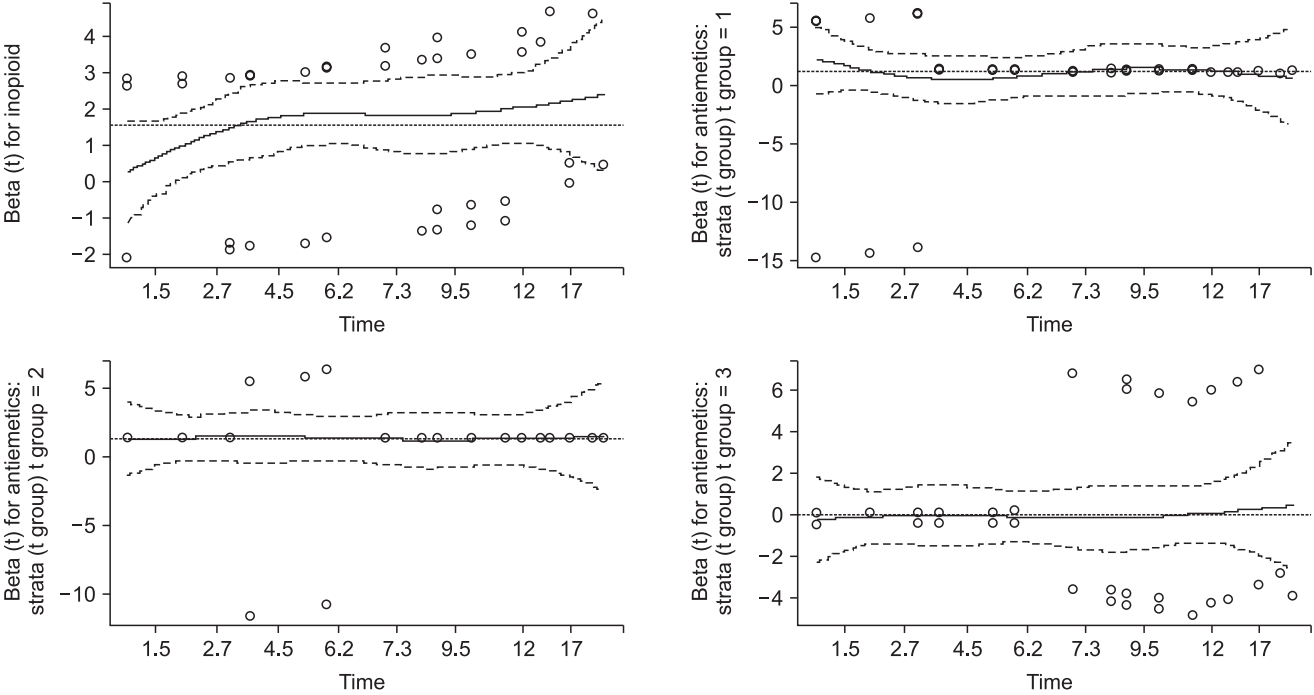
A Schoenfeld residual test is shown below. Here, ‘cox.zph’ included in the ‘survminer’ library enables this test. The results are listed in Table 6, and graphical output is shown in Fig. 6.
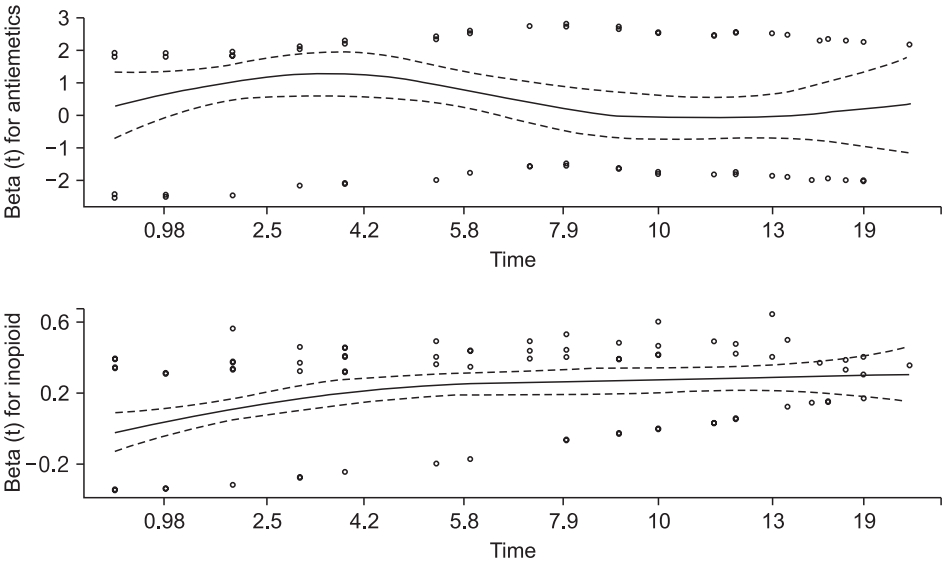
Schoenfeld residual plot with ‘Antiemetics’ and ‘Inopioid’. Dotted horizontal lines indicate the estimated coefficient values of these covariates.
# Schoenfeld residuals test
sf.residual <- cox.zph(cph.selected)
print(sf.residual) # display the results
par (mfrow = c(2,1))
plot(sf.residual[1]) # plot curves
abline (h = coef(cph.selected)[1]
, lty = "dotted", lwd = 1)
plot(sf.residual[2])
abline (h = coef(cph.selected)[2]
, lty = "dotted", lwd = 1)
The P value in Table 6 indicates the significance probability of the Schoenfeld residual test for the antiemetics and intraoperative opioid used, and such values indicate a violation of the proportional hazard assumption. A positive increment of the Schoenfeld residual curve for ‘Inopioid’ is shown in Fig. 6. The curve for the antiemetics gradually changes toward a negative value over time, but not continuously. In this way, a Schoenfeld residual test provides more objective results than an LML plot, which is strictly conservative.
Adding a time-dependent covariate
To validate a proportional hazard assumption in a CPH model, a time-dependent covariate is intentionally added into the estimated model. This covariate can be made using a time-independent variable and time, or a function of time. For example, the process compares two models, namely, a CPH model that assumes the proportional hazard assumption has not been violated, and another model incorporated with a combined covariate of the explanatory variable and time (or a function of time) in the estimated CPH model. A likelihood ratio test or Wald statistics are used for comparison. This type of method has certain advantages, including a simultaneous comparison with multiple covariates and various time functions; note that the results may change depending on the covariates and types of functions selected [5,10,11].10)
Cox Proportional Hazard Regression Models with Time-dependent Covariates
Covariates violating the proportional hazard assumption in a CPH model should be adequately adjusted. This section introduces a stratification and time-dependent Cox regression to deal with covariates violating the proportional hazard assumption.
Stratified Cox proportional hazard model
To fit the CPH model with variables violating the proportional hazard assumption, one method is to apply a stratified CPH model. This method makes one integrated result from the results of each stratum containing a categorical variable classified based on a certain criterion. Unlike the Mantel–Haenszel method, which is based on the sample size of each stratum, stratification in the CPH model sets a different baseline hazard corresponding to each stratum, and a statistical estimation is then applied to achieve common coefficients for the remaining explanatory variables except for the stratified variables.11,) This provides a hazard ratio of the controlled effects of variables violating the proportional hazard assumption [12].
A stratified CPH model can be applied to control the variables violating a constant hazard assumption, as well as to control the confounding factors that influence the results with little or no clinical significance. Stratification always requires categorical variables, and conversion into categorical variables is required for continuous variables. Under this situation, care should be taken that the sample size of each stratum is reduced (data thinned out) and information held by the continuous variable is simplified. Therefore, conversion into a categorical variable should consider as small number of strata as possible, setting the range of clinical or scientific meaning, and maintaining a balance among the strata [12].
R codes for stratified Cox proportional hazard model
In the previous CPH modeling, the variable ‘Inopioid’ violated the constant hazard assumption based on the Schoenfeld residual test (Fig. 6). Here, ‘Inopioid’ is a continuous variable that records the dose of intraoperatively used opioid. To apply a stratified CPH modeling, continuous variables should be converted into categorical variables. For convenience, the following is a code that converts ‘Inopioid’ into a categorical variable of 0 or 1, when not used or used, respectively.
##### Stratified Cox regression
### Add categorical variables from Inopioid
PONV.raw <- transform(PONV.raw,
Inopioid_c = ifelse(
Inopioid == 0, 0, 1))
head (PONV.raw)
According to this, the categorical variable ‘Inopioid_c’ is recorded as 0 or 1 and is newly added to the dataset (Table 7).
Next, the code for a stratified CPH model is as follows:
### Stratified Cox proportional hazard modeling
cph.strata <- coxph (Surv(Time, PONV == 1)
~ Antiemetics + strata(Inopioid_c)
, data = PONV.raw)
summary (cph.strata)
ggsurvplot(survfit(cph.strata)
, data = PONV.raw
, risk.table = TRUE
, palette = c("black","black")
, linetype = c("solid","dashed")
)
par( mfrow = c(1,1))
plot (survfit(cph.strata)
, fun = "cloglog"
, main = "Antiememtics"
)
sf.residual.strata <- cox.zph(cph.strata)
print(sf.residual.strata)
plot(sf.residual.strata)
abline (h = coef(cph.strata)
, lty = "dotted"
, lwd = 1)
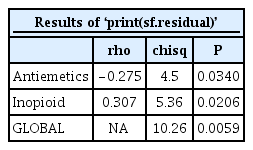
This code outputs a stratified CPH model by controlling ‘Inopioid_c’ (Table 8). The command ‘ggsurvplot’ provides survival curves of two strata and prints the LML plot using the last ‘plot’ command (Fig. 7). The Schoenfeld residual test using a ‘cox.zph’ command reveals that ‘Antiemetics’ violates the proportional hazard assumption (rho = −0.265, chisq = 4.26, P = 0.039, shown in Fig. 8). It is possible to obtain an adequate CPH model by stratifying ‘Inopioid’ and ‘Antiemetics’, although the interpretations may be complex because it is difficult to integrate the comparison results among all strata.
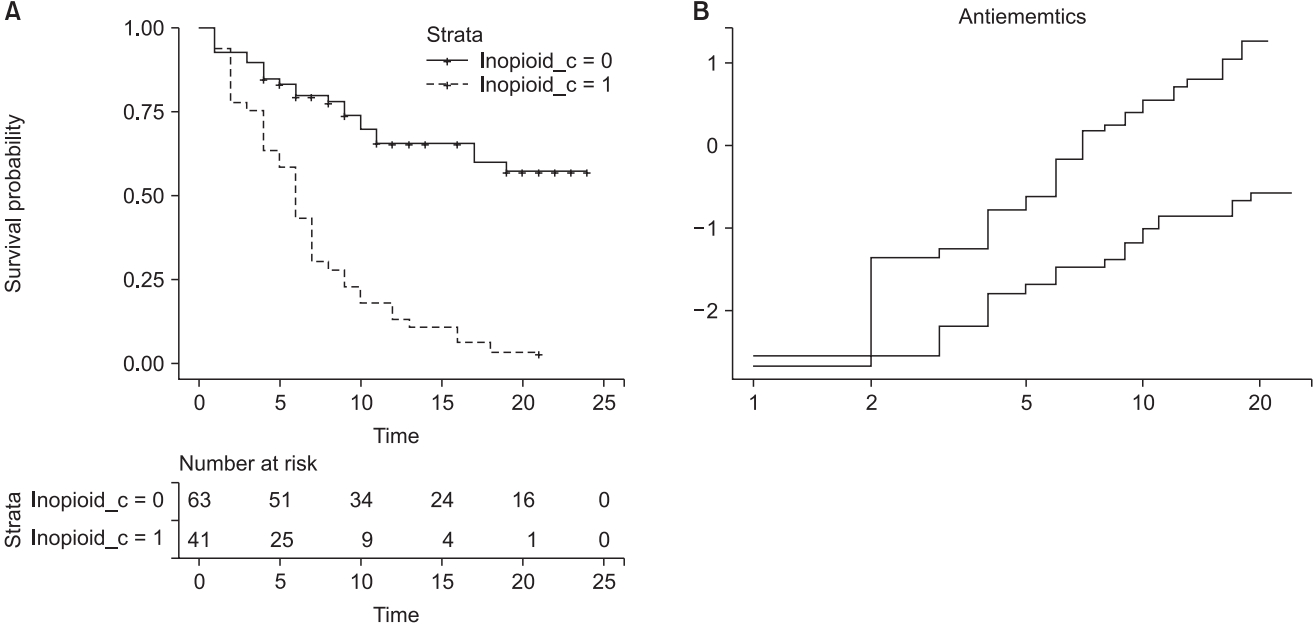
Examples of the stratified Cox proportional hazard model and corresponding LML plot. (A) Survival curves of estimated stratified Cox proportional hazard model. Stratification is achieved using the categorical variable ‘Inopioid_c’. (B) Log-minus log plot for evaluation of proportional hazard assumption against two antiemetics. Note that a non-parallelism of below 2 h is not assured, whereas the overall curves are roughly parallel without crossing.
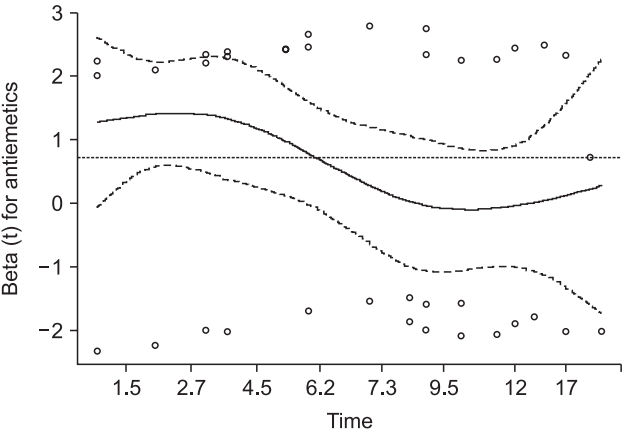
Schoenfeld residual test for the stratified Cox proportional hazard model. For the covariate ‘Antemetics’, the probability was estimated as 0.039, and a violation of the proportional hazard assumption was strongly suggested under the controlled covariate ‘Inopioid’ (the dotted horizontal line shows the estimated coefficient of ‘Antiemetics’).
Time-dependent Cox regression
Most clinical situations change over time, and the variables affected by a specific treatment also change even when the treatment remains constant during the observation period [13]. For example, consider an analgesic having a toxic effect on the hepatobiliary function for patients with chronic pain. A periodic liver function test will be crucial, and all laboratory results will vary for every follow-up time. The administration dose may also vary according to the laboratory results or analgesic effects. Moreover, the laboratory results may not be valid after the patients are censored or after an event occurs. These variables are common in clinical practice, and the existence of time-dependent variables should be considered and checked before starting the data collection for survival analysis. If an adequate measurement method is developed, a time-dependent covariate Cox regression will be possible. Another type of time-dependent variable is a covariate with a time-dependent coefficient [14]. If the analgesics mentioned above produces a level of tolerance, its effect decreases over time. This indicates that the risk of breakthrough pain occurrence may be higher as time passes, which apparently violates the proportional hazard assumption. In this case, the effect of the analgesics can be included in the survival function, which is expressed as a covariate with a coefficient of the function of time.
As mentioned above, a time-dependent covariate is incorporated into the analysis as a single value according to the repeated observation intervals. For example, a patient under analgesics medication takes an initial liver function test, the results of which show 40 IU/L and 100 IU/L after four weeks with continued pain and 130 IU/L at eight weeks with pain, whereas at 12 weeks after analgesics administration, the pain is subsided and medications are discontinued without a further laboratory test. The laboratory data input for the time-dependent covariate are 40 until 4th weeks without an event, 100 from 4th to 8th weeks without an event, 130 from 8th to 12th weeks, and an event occurs at 12th weeks.
Clinical studies in the area of anesthesiology often include variables related to the response or effect of a specific treatment or medication. Depending on the characteristics and measurement methods of the variables, once a specific treatment or medication is applied, their effects are gradually decreased over time or delayed until the onset time. The effects of treatment or medication changes over time, the coefficient of these effects can be expressed as a time function, and for Cox regression, a step function is frequently applied. A step function is a method applying different coefficient values to different time intervals. A Cox regression can thus be established and output the integrated results [15]. In addition, a continuous parametric function for a time-dependent coefficient can be used for analysis instead of a step function [14].
R code for time-dependent coefficient Cox regression model: step function
As shown in Fig. 6, the Schoenfeld residuals of ‘Antiemetics’ and ‘Inopioid’ turn from positive to negative or vice versa at approximately 3 and 6 h. The data are arbitrarily separated using these time points.
tdc <- survSplit (Surv(Time, PONV) ~.
, data = PONV.raw
, cut=c(3, 6)
, episode = "tgroup"
, id = "id"
)
head(tdc)
The command ‘survSplit’ separates the patient data according to the established time interval, where the value for each interval is the measured value on the left side of the interval (start time, ‘tstart’), and ‘Time,’ which is the end of the interval succeeds the next interval. That is, one interval is closed at the left and opened at the right, and if an event occurs during the interval, the survival function is estimated using the variables measured at the left side of the interval (Table 9). It seems that the data being duplicated at the end and the start of the interval, problems do not occur because the divided time does not overlap. It is possible to apply a Cox regression and GOF test with these separated data.
# Fitting Cox regression
fit.tdc <- coxph(Surv(tstart,Time, PONV)
~ Antiemetics:strata(tgroup)
+ Inopioid
, data = tdc)
summary(fit.tdc)
# GOF test
sf.tdc <- cox.zph(fit.tdc)
print (sf.tdc)
par(mfrow=c(2,2))
plot(sf.tdc[1])
abline (h = coef(fit.tdc)[1], lty = "dotted")
plot(sf.tdc[2])
abline (h = coef(fit.tdc)[2], lty = "dotted")
plot(sf.tdc[3])
abline (h = coef(fit.tdc)[3], lty = "dotted")
plot(sf.tdc[4])
abline (h = coef(fit.tdc)[4], lty = "dotted")
Table 10 shows the estimated Cox regression and GOF test results, and Fig. 9 presents a plot of the Schoenfeld residuals. The risk of the PONV increases 1.0126-fold (95% CI: 1.0078–1.017, P < 0.001) by one unit of intraoperative opioid. For the antiemetics, the group taking drug B showed an increased PONV risk of 3.6545-fold (95% CI: 1.2024–11.107, P = 0.022) until 3 h post-operation, 3.8969-fold (95% CI: 1.4020–10.831, P = 0.009) until 6 h post-operation, with no significant difference shown until the end of the observation (risk ratio = 0.9382, 95% CI: 0.4242–2.075, P = 0.957). The results of the Schoenfeld residual test (Table 10 and Fig. 9) indicate that all variables do not violate the proportional hazard assumption. These results cannot provide a single desired outcome, and it is necessary to combine the results.

Results of Time-dependent Coefficient Cox Regression Using Step Function and Schoenfeld Residual Test
# Combined results
combine.tdc <- data.frame(tstart = rep(c(0,3,6), 2)
, Time = rep(c(3,6, 24), 2)
, PONV = rep(0,12)
, tgroup= rep(1:3,4)
, trt = rep(1,12)
, prior= rep(0,12)
, Antiemetics = rep(c(0,1), each = 6)
, Inopioid = rep (c(0,1), each = 3)
, parameter = rep(0:1, each = 6)
)
combine.tdc
cfit.tdc <- survfit(fit.tdc
, newdata = combine.tdc
, id = parameter
)
cfit.tdc
km <- survfit(Surv(Time, PONV) ~Antiemetics
, data = PONV.raw
)
summary (km)
km
par( mfrow = c(1,1))
plot(km, xmax= 24, col="Black"
, lty = c("solid","dashed"), lwd=2
, xlab="Postoperative hours"
, ylab="PONV free"
)
lines(cfit.tdc, col="Grey"
, lty= c("solid","dashed"), lwd=2)
legend (x = 0.15, y = 0.25
, c("Drug A, Kaplan-Meier estimation"
, "Drug B, Kaplan-Meier estimation"
, "Drug A, Cox regression with time-dependent coefficient"
, "Drug B, Cox regression with time-dependent coefficient"
)
, col = c("black", "black", "grey", "grey")
, lty = c("solid", "dashed", "solid", "dashed")
)
To compare the results from two antiemetics, the data divided by ‘survSplit’ are combined to enable an interpretation (combine. tdc). The results are shown in Table 11. The survival model considering the time-dependent coefficient increases the sample size because the data of one patient are separated at the established time points. Note that the median survival times in this model are 31 and 16 h, and the median survival times from the Kaplan–Meier analysis are 13 and 6 h. Plotting these two models into a single graph enables a visual comparison (Fig. 10). Here, although ‘ggsurvplot’ provides comprehensive graphs, it cannot draw two graphs simultaneously. Another graphics software is required to make a single graph from these graphs (Fig. 11).

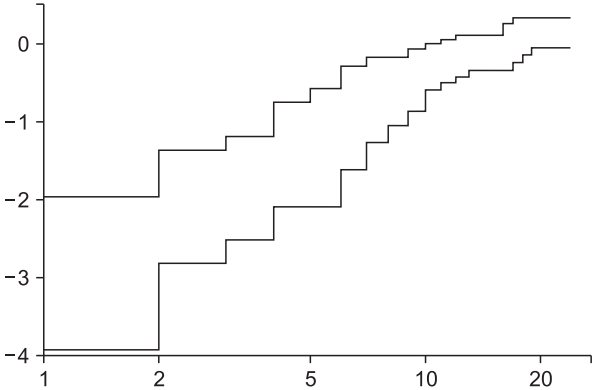
Graphical comparison between survival models of Kaplan– Meier and Cox regression with time-dependent coefficient. Black curves indicate the model fitted using a Kaplan–Meier analysis, and the gray curves are from a Cox regression with a time-dependent coefficient. The solid lines indicate Antiemetics = 0 (Drug A), and the dashed lines indicate Antiemetics = 1 (Drug B).

Cox regression model with the time-dependent coefficient. Survival curves of Kaplan–Meier analysis (A) and time-dependent coefficient (B) using ‘ggsurvplot’ command. Gray solid lines indicate Antiemetics = 0 (Drug A), and the black dashed lines indicate Antiemetics = 1 (Drug B). The results of the survival analysis are changed when considering the constant hazard ratio assumption.
## plot using ggsurvplot
ggsurvplot ( km, data = PONV.raw,
fun = "pct", pval = TRUE,
conf.int = TRUE, surv.median.line = "hv",
linetype = "strata", palette = "grey",
legend.title = "Antiemetics",
legend.labs = c("Drug A", "Drug B"),
legend = c(.1, .2), break.time.by = 4,
xlab = "Time (hour)",
risk.table = TRUE, tables.height = 0.2,
tables.theme = theme_cleantable(),
risk.table.y.text.col = TRUE,
risk.table.y.text = TRUE
)
ggsurvplot ( cfit.tdc, data = PONV.raw,
fun = "pct",
conf.int = TRUE, surv.median.line = "hv",
linetype = "strata", palette = "grey",
legend.title = "Antiemetics",
legend.labs = c("Drug A", "Drug B"),
legend = c(.1, .2), break.time.by = 4,
xlab = "Time (hour)",
risk.table = TRUE, tables.height = 0.2,
tables.theme = theme_cleantable(),
risk.table.y.text.col = TRUE,
risk.table.y.text = TRUE
Conclusions
Clinical studies in the area of anesthesiology had rarely presented statistical results using survival analysis. In recent years, studies on the survival or recurrence of cancer according to the anesthetics have been actively published [16–18]. Survival analysis has the power to present clear and comprehensive results based on studies on pain control or the effects of medications. Previous articles have focused on the basic concepts of survival analysis and interpretations of the published results [1], and the present article covered the process of conducting a survival analysis using clinical data, finding errors, and achieving adequate results. Although this article does not include all existing survival analysis methods, it introduced several R codes to enable an intermediate level of survival analysis for clinical data in the field of anesthesiology.12)
Some clinical papers dealing with a survival analysis have presented statistical results without considering a proportional hazard assumption or an interaction between the covariates and time. The power of a log-rank test, which is commonly used to compare two groups, tends to decrease when a proportional hazard assumption is violated and can generate an incorrect result [19,20]. An investigation into the reporting of survival analysis results in leading medical journals indicated that the use of survival analysis has significantly increased, although several problems still exist, including descriptions regarding the censoring, sample size calculation, constant proportional hazard ratio assumption validations, and GOF testing [21]. Because most statistical analyses require several basic assumptions, survival analysis also requires some essential assumptions. In a Kaplan–Meier analysis, the likelihood of an event of interest and censoring occurring should be independent from each other, and the survival probabilities of patients who participated in earlier and later studies should be similar. A log-rank test also requires the previously described and proportional hazard assumptions [22]. A CPH model requires a proportional hazard assumption, independence between the survival times among different patients, and a multiplicative relationship between the predictors and hazard [23].
When reporting or interpreting the results of survival analysis, it is important that the identification of the underlying assumptions corresponds to the statistical analysis, and it is necessary to verify that the assumptions are reasonable and well maintained. Statistical results with violated assumptions cause deviated decisions because of an increased probability of error. Survival analysis will be a powerful tool to achieve a scientific conclusion when an appropriate method is chosen with regard to the nature of the variables, the relationship with time, and other basic assumptions.
Notes
Sample data (Survival2_PONV.csv) and the R console output of entire code are provided as supplemental information. Refer to online help or R statistical textbooks for detailed explanations of the argument. The included R code covers the process beginning with the survival analysis introduced in [1]. A detailed description of a violation of a proportional hazard assumption is provided in [14].
Terry M. survival: Survival Analysis. R package version 2.42-4. 2018. https://github.com/therneau/survival.
Alboukadel K, Marcin K, Przemyslaw B, Scheipl F. survminer: Drawing Survival Curves using 'ggplot2', R package version 0.4.3. 2018. http://www.sthda.com/english/rpkgs/survminer/.
There are several ways to draw an LML plot in R; ‘plot.survfit’ with the argument ‘fun = “cloglog”’ provides an LML plot of the log-scaled x-axis. Most statistical references describe a log-scaled x-axis LML plot, whereas others describe a standard linear-scaled x-axis LML plot. The R code for a non-log-scaled LML plot can be created through the following. # Non-log scaled LML plot ponvsurv=Surv(PONV.raw$Time, PONV.raw$PONV) NLML.fun=function(p){return(log(-log(p)))} plot (survfit(ponvsurv ~ PONV.raw$Antiemetics), fun=NLML.fun)
R package ‘survival’ version 2.44-1 (updated in March 2019) has an error with an x value of 1 when log scaled using the x-axis. Versions before 2.44-1 work properly.
Schoenfeld residual is only for the patient who experienced the event. It is the difference between observed value of explanatory variable at a specific time and expected value of the explanatory variable (covariate) at a specific time which is a weighted-average value by likelihood of event from the risk set at that time point.
Some statistical software provides a method using scaled Schoenfeld residuals. Under a specific circumstance, these two results are different, although they mostly produce similar results. Please refer to the following: Grambsch, P.M. and Therneau, T.M. 1994. Proportional hazards tests and diagnostics based on weighted residuals. Biometrika 81: 515-526.
The command ‘ggadjustedcurves’ included in the ‘survminer’ library easily produces the survival curves of the CPH model. Unfortunately, this command still has minor functional errors such as in printing the 95% CI or labelling, and a somewhat complex ‘ggsurvplot’ is used in this example.
In R, categorical variables should be treated as a stratum for comparison using an LML plot of the CPH model.
Because various application methods and their variations are available, they are not discussed in detail herein.
This is a non-interaction stratified CPH model. Several survival functions are estimated through stratification, and if the explanatory variables have interactions with each other, the coefficients at each stratum may be different. In this case, it is assumed that an interaction model between explanatory variables and a likelihood ratio test provide clues to judge whether there is an interaction between explanatory variables. That is, if two or more variables are included in the model, it is necessary to check whether an interaction between them exists.
A clustered event time analysis and an accelerated failure time analysis are often applied to survival analysis methods in clinical study. A clustered event time analysis is similar with a stratified CPH model, and has certain advantages when each stratum has insufficient event cases. It has two types of processes, one is a marginal approach that estimates the survival function through an overall cluster from the pooled effect of each stratum, and another is a conditional approach that estimates the survival function from the heterogeneity between clusters. An accelerated failure time analysis estimates the model similarly with a linear regression based on a Weibull distribution or log-logistic distribution. Unlike a CPH model that continuously maintains the risk ratio of the covariates, this model assumes that the disease process can be accelerated or decelerated over time.
Notes
Conflicts of Interest
No potential conflict of interest relevant to this article was reported.
Author Contributions
Junyong In (Conceptualization; Writing–original draft; Writing–review & editing)
DDong Kyu Lee (Conceptualization; Writing–original draft; Writing – review & editing)
Supplementary Materials
Futher detailes are presented in the online version of this article (Available from https://doi.org/10.4097/kja.19183).