Introduction
Usually more than two different types of nondepolarizing muscle relaxants (NDMRs) are not administered at the same time. However, the administration of nondepolarizing muscle relaxants in combination was introduced by Lebowitz et al. [
1] to reduce individual drug dosages and to decrease the side effects. Combinations of rocuronium and cisatracurium allow rapid induction and have been reported to exhibit synergistic effects, despite the limitations of limited dose combination and lack of consideration of the biophase interaction. Kim et al. [
2] demonstrated synergistic interaction between cisatracurium and mivacurium, atracurium, vecuronium or rocuronium when they were co-administered. Naguib et al. [
3] concluded that the interaction between rocuronium and cisatracurium was synergistic on isobolographic analysis, and Breslin et al. [
4] reported prolonged clinical duration of the maintenance dose of cisatracurium after induction with rocuronium.
To cover the full range of interaction between the two drugs in the biophase, a response surface model should be used rather than traditional isobolographic analysis. Response surface modeling provides the entire range of isobolograms and effect site concentrations at the given pharmacodynamic endpoints. Since Sheiner et al. [
5] conducted pioneering work on the pharmacokinetics (PKs) and pharmacodynamics (PDs) of neuromuscular blocking agents, population models of rocuronium and cisatracurium have revealed not only their pharmacokinetics but also the relationships between effect site concentrations and pharmacodynamic endpoints. PD models enhance prediction of the time course of effect site concentration of NDMRs and their pharmacodynamic endpoints, as determined by Train-of-four (TOF) ratio or T1% values.
Several population-derived response surface interaction models are available, and the Greco model is considered as a more basic approach since it was devised first and it is the simplest model. The Minto model, which is an extension of the Greco model, is more flexible. These models define drug ratio as the proportion of one drug in the combination and treat drug combinations as individual drugs.
This study was performed to address the hypothesis that rocuronium and cisatracurium exhibit pharmacodynamic synergism in terms of muscle relaxation, and to quantify the pharmacodynamic interaction between these two drugs using the response surface model.
Materials and Methods
This study was performed using a randomized, prospective, open-label design. After obtaining Institutional Review Board approval and informed consent, 120 patients classified as American Society of Anesthesiologists physical status I or II, females, aged from 30 to 60 years, and scheduled for elective thyroidectomy or mastoidectomy were enrolled. None of the study subjects had a renal, hepatic, or neuromuscular disease, a metabolic abnormality, or were being treated with any drug that could interfere with neuromuscular block, such as magnesium. All patients were premedicated with glycopyrrolate 0.2 mg and midazolam 2–3 mg IM.
In the operating room, electrocardiogram, pulse oximetry, noninvasive blood pressure, esophageal stethoscope temperature, and entropy were monitored. Esophageal temperature was maintained above 35oC. Anesthesia was induced and maintained by TCI infusion of propofol (2.5–4.5 µg/ml) and remifentanil (1.0–6.0 ng/ml) based on the pharmacological models of Marsh and Minto, respectively [
6,
7]. Appropriate depth of anesthesia was achieved by maintaining BIS in the range of 40–60. Ventilation was adjusted to maintain normocapnia using an end-tidal carbon dioxide pressure of 30–40 mmHg. If patient movements were noted before full recovery, it was planned to administer a rescue dose of rocuronium 0.1 mg/kg and the study case was scheduled to be closed.
Drug administration
These 120 study subjects were randomly allocated to receive one of the fifteen predefined combinations of rocuronium and cisatracurium using a radial combination dosing schedule (
Fig. 1). To study single drugs, cisatracurium 0.2, 0.15 or 0.1 mg/kg (A1, B1 or C1) or rocuronium 0.8, 0.6 or 0.4 mg/kg (A5, B5 and C5) doses were administered alone. For drug combinations, three types of combination ratio were applied; (1) half of each single dose of both drugs (A3, B3 and C3) (2) 75% of each single dose of rocuronium and 25% of each single dose of cisatracurium (A2, B2 and C2), and (3) 25% of each single dose of rocuronium and 75% of each single dose of cisatracurium (A4, B4 and C4). Eight patients were allocated to receive each single and combination dose.
Predetermined doses of both drugs were injected intravenously by rapid injection. In the case of combined administration, cisatracurium was injected first and then rocuronium was injected immediately after cisatracurium injection.
Neuromuscular monitoring
Neuromuscular monitor (NMT MechanoSensor, DATEX-OHMEDA/GE HEALTHCARE, Helsinki, Finland) was applied to the adductor pollicis, which is innervated by the ulnar nerve. The monitored arm was immobilized and the thumb was protected to allow free response to stimulation. After loss of consciousness was produced, to detect the supramaximal stimulus current, the equipped process of NMT MechanoSensor, supplied by the manufacturer, was used. After 2 to 3 minutes of recording stabilization, predetermined NDMRs were administered. TOF stimulation was performed and TOF ratio (first twitch/fourth twitch) and Tl% responses (percentage compared to the initial T1) were measured.
T1% response after complete recovery often did not return to the initial level. When this occurred, a correction factor F was applied to obtain the corrected T1% [
8]:
where T1%start is the first T1% value after calibration and T1%end is the T1% value at complete recovery. Corrected T1% was T1% multiplied by F. Corrected T1% values were obtained only for the recovery phase.
During the time period starting from injection of the muscle relaxant until the end of intubation, data were recorded every 10 seconds, and then data were recorded every 20 seconds during the maintenance and full recovery from muscle relaxation.
Biophase concentration
To predict effect site concentrations, we used the PKPD model for rocuronium and cisatracurium. The following criteria were used for selecting the models: first, reports should present ke0 with the PK model simultaneously, second, TOF ratio or T1% should be recorded as a surrogate marker of muscle relaxation and either of them should be applied in both rocuronium and cisatracurium models simultaneously, and third, propofol should be administered as the main anesthetic for all PKPD models rather than as an inhalation anesthetic.
T1% values were fitted with effect site concentrations of rocuronium and cisatracurium predicted by the PKPD model as reported by Fernández-Candil et al. [
9] and Tran et al. [
8], respectively. The model reported by Kleijn et al. [
10] was chosen as a PKPD model for predicting effect site concentrations of rocuronium. The parameters of PKPD models predicting effect site concentration of rocuronium and cisatracurium are listed in
Table 1.
Interaction model
The response surface model described by Greco et al. [
11] and Minto et al. [
12] was used to analyze the interaction. The Greco model was implemented with the normalized combined concentration NCC:
where Cer and Cec are the effect site concentrations of rocuronium and cisatracurium, respectively, Ce50,r and Ce50,c are the effect site concentrations of rocuronium and cisatracurium that produce 50% maximal effects, respectively, and α is the interaction coefficient. When α > 0, the drug interaction is synergistic; when α < 0, the drug interaction is antagonistic; and when α = 0, the drug interaction is additive. A larger positive α indicates stronger synergy. To assess the significance of α, we investigated whether the 95% confidence interval of α included 0 or not.
NCC was implemented in the inhibitory full sigmoid E
max model for both TOF ratio and T1%:
where E0 is the effect when no drug is given, Emax is the maximal effect of a drug combination, and γ is the dose response curve slope.
For the Minto model [
12], drug concentrations were normalized versus corresponding C
e50 values.
Where Uroc and Ucis are normalized concentrations with respect to Ce50 for each drug, Ce50,r and Ce50,c are the effect site concentrations of rocuronium and cisatracurium that produce 50% of maximal effects, respectively.
A new variable θ was defined using normalized concentrations to represent the ratio of rocuronium to the combination drug:
θ values range from 0 to 1. When rocuronium is administered alone, Ucis = 0, and hence θ = 1. Conversely, when cisatracurium is administered alone, Uroc = 0, and hence θ = 0. When same normalized concentrations of both drugs are administered, θ = 0.5.
A new variable U(θ) representing the normalized unit of concentration was defined as follows:
where U50(θ) is the normalized unit of concentration that produces 50% of the maximal effect at a ratio of θ.
Finally, the following Hill equation can be obtained by substituting the above terms into the inhibitory full sigmoid Emax model:
where E0 is the baseline effect with no drug, Emax(θ) is the maximum possible drug effect at ratio θ, and δ(θ) is the steepness of concentration-response relationship at ratio θ. Each drug ratio can have its own U50 and δ, and hence each of the ratios behaves as a single drug with its own sigmoidal concentration–response relationship. However, in this study, Emax was fixed at 0 at all θ ratios and δ was assumed to be identical at all ratios.
To define U50(θ), second-order polynomial functions were implemented:
where β are coefficients that define the relationships with U
50(θ) at each θ ratio. Additivity of the interaction can also be defined with β. That is, when β > 0, the drug interaction is synergistic; when β < 0, the drug interaction is antagonistic; and when β = 0, the drug interaction is additive [
13].
Parameter estimation
To estimate parameters, we implemented the naive pooled data approach using NONMEM® (version 7.2, Icon Development Solutions, Ellicott City, MD, USA). All parameters are reported as typical values and relative standard errors (percentages) of typical values and 95% confidence intervals.
Results
A total of 99 patients were included in the study. Mean subject age, weight, and height were 48.1 ± 8.8 years (range, 30–60 years), 59.2 ± 9.2 kg (range, 43–85 kg) and 158 ± 4.9 cm (range, 145–172 cm), respectively, and mean creatinine value was 0.66 ± 0.09 mg/dl (range, 0.49–0.93 mg/dl). Twenty-one patients were dropped out; 2 cases due to dosing error, 4 cases due to surgeries that ended before full recovery, 9 cases due to an error in the data collection program, and 6 cases due to interruption of the free finger movement by surgeons who leaned on the patient's arm. The number of drop out cases was one at B1, B2, B4, C3 and C5; two at A4, A5, B3, B5, C1 and C4; and four at A3.
The parameters of PKPD models predicting the effect site concentration of rocuronium and cisatracurium are listed in
Table 1. However, it was difficult to find a PD model for cisatracurium that was related to TOF ratio values for the prediction of effect site concentrations. Therefore, the ke0 value of the Tran model was modified by fitting TOF ratio values obtained from a single dose group of cisatracurium with plasma concentration predicted by the Tran PK model. The ke0 of cisatracurium was found to be 0.0613 when TOF ratio was measured as a surrogate marker for the response to cisatracurium.
The results of pharmacodynamic parameters and interaction modeling are shown in
Table 2. According to the interaction model of Greco et al. [
11], the interaction term 'α' for TOF ratio and T1% was 0.977 and 1.12, respectively. Both values were positive and the 95% confidence interval did not include zero, which means that α was significantly different from zero and the drugs exhibited a synergic interaction. The β interaction term of the Minto model resulted in positive coefficients of 0.715 and 0.786 for TOF ratio and T1% measurements, respectively. The U
50(θ) values of TOF ratio and T1% measurements were positive in the range 0 < θ < 1 and showed an upward concave plot of < 1, which means that the drugs acted synergistically (
Fig. 2).
The response surfaces of the Greco and Minto model are plotted in
Figs. 3 and
4, respectively, with their own isoboles, which produce 10, 50, and 90% of the maximum estimated T1% or TOF ratio values. For both models, the concave to outward response surfaces exhibited a curvature, indicating synergism. On isobolograms, the dashed line represents theoretical additivity, whereas the solid line shows combinations of effect site concentrations of the two drugs that achieve the same effect. The left downward convexity of the solid line demonstrates the synergistic nature of the interaction.
Discussion
The results of this study confirm that rocuronium and cisatracurium exhibit pharmacodynamic synergism with respect to neuromuscular blocking effects as determined by using TOF ratio or T1% as surrogate markers.
The interaction term of the Greco model remained fixed regardless of the drug ratio used during model building, indicating that synergism occurred at all drug combination ratios. However, the Minto model assumes that different drug ratios can be treated as separate drugs with their own U
50 and δ values. Based on this assumption, U
50 could be presented as a function of combination ratio as shown in
Fig. 2. At ratios of 0 and 1, U
50(θ) should be 1, and between ratios 0 and 1, it should be less than or greater than 1. Theoretically, additivity is defined as a U
50(θ) value of 1. However, a 10% degree of deviation in measurement of the parameters should be taken into consideration; hence, the additive interaction was considered to exist when U
50(θ) was between 0.9 and 1.1 [
13,
14]. In the current Minto model, the θ ratio, which corresponds to U
50(θ) < 0.9, is between the ratio 0.17 and 0.83 for the TOF ratio model and between the ratio 0.15 and 0.85 for the T1% model (
Fig. 2). It is important that the θ ratio should not be misunderstood as the ratio of the amount of intravenously administered doses. The θ ratio is the predicted concentration ratio of the two drugs at the effect site regardless of the ratio of the amount of intravenously administered doses.
For the Greco interaction model, the larger is the positive interaction term α, the stronger would be the interaction of the two drugs. The results of the current study did not show such a large number for interaction terms. However, there were no criteria specifying how large the interaction term should be to detect synergism. Even though the interaction term has a large positive number, it should only be additive unless the confidence interval of the interaction term excludes zero. In a propofol and remifentanil interaction study, Kern et al. [
15] reported various interaction terms ranging from 5.1 to 33.2 according to the measurements of drug effects which include sedation and response to laryngoscopy. Regarding the Minto interaction term β, Diz et al. [
14] reported it as a positive number of 0.424; however, they only concluded that additivity exists because the β value did not differ significantly from the value of 0 due to its wide confidence interval. Heyse et al. [
16] reported the interaction term β between sevoflurane and remifentanil as 1.47, which turned to be significant.
This study has various limitations that need to be mentioned. A few of them are attributable to the use of the already established population PKPD model to predict effect site concentrations rather than direct blood sampling and measurement. Furthermore, when published population models are utilized, the characteristics of the subjects being investigated should be the same as those of the population models used, which is almost impossible in practice. In addition, the populations of the rocuronium and cisatracurium models used in the current study do not coincide with each other.
A volunteer study based on a crossover design could provide an opportunity to investigate the entire spectrum of drug interactions, from very low to high concentrations. However, combinations of low doses that do not induce clinically required muscle relaxation could not be investigated in the current study because the study subjects were not treatment-naive volunteers but they were patients scheduled for surgery.
There have been several studies which investigated PD models with same muscle relaxants, and the results, especially the ke0 value, differ from case to case. This results not only from the different populations used but also from the different modalities and surrogate markers which were used to measure the clinical effects of muscle relaxants. Acceleromyography, mechanomyography and electromyography should not be used interchangeably [
17,
18] as the ke0 values derived from different modalities result in different values. Different clinical endpoints like T1% and TOF ratio could cause discrepancies in the ke0 values between studies.
These limitations are inevitable when the institutional review board does not approve blood sampling, and the only option for the current study is the application of model-predicted drug concentrations. To reduce the error which results from the application of model-predicted drug concentrations, a few efforts were made such as using the same anesthetic as in the referred model and selecting the model with covariate modeling. Despite these limitations, the results of this study could be considered well defined as they show a small relative standard error in most of the parameters.
In conclusion, this study suggests that Greco or Minto response surface modeling and the derived coefficient of the interaction term demonstrated synergism between rocuronium and cisatracurium based on TOF ratio and T1% measurements.
Fig. 1
Design for drug combination. A1, B1, and C1 and A5, B5, and C5 represent single doses of rocuronium and cisatracurium, respectively. Three radial lines represent different rocuronium and cisatracurium combination ratios; half doses of the two drugs are represented by A3, B3 and C3, 75% doses of rocuronium and 25% doses of cisatracurium are represented by A2, B2 and C2, and 25% doses of rocuronium and 75% doses of cisatracurium are represented by A4, B4 and C4.

Fig. 2
Plots of U50 of T1% (A) and TOF (B) as a function of θ showed upward concave features, indicating a synergistic interaction between the two drugs. Given a measurement variability of up to 10%, solid lines below the dashed line at 0.9 were considered to indicate synergism. U50(θ): the normalized unit of concentration that produces 50% of the maximal effect at a ratio of θ which is the ratio of normalized concentrations of rocuronium to the normalized combination drug.

Fig. 3
Response surfaces and isoboles of the Greco (A, C) and Minto (B, D) model for T1% 10, 50, and 90% of the maximum effect as a function of rocuronium and cisatracurium effect site concentrations. Isoboles of combined drugs showed a synergistic effect (solid line). Theoretical additive lines are shown as dashed lines.
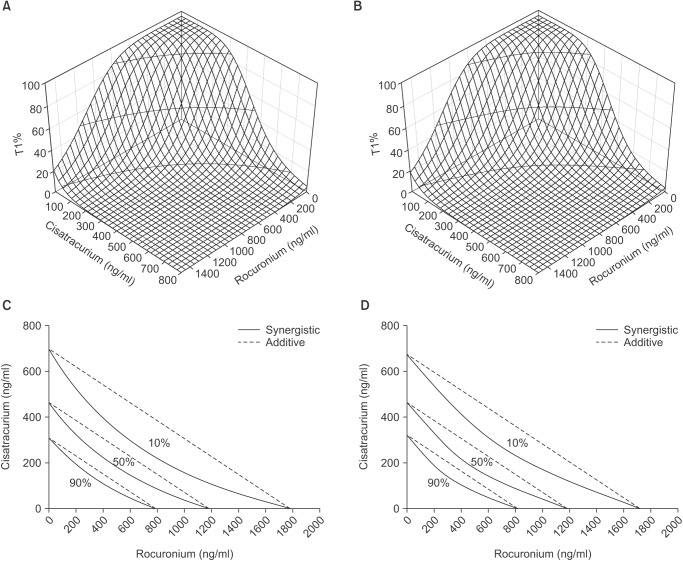
Fig. 4
Response surface and isoboles of the Greco (A, C) and Minto (B, D) model for TOF ratio 10, 50, and 90% of the maximum effect as a function of the effect site concentrations of rocuronium and cisatracurium. Isoboles of the drug combinations showed a synergistic effect (solid line). Theoretical additive lines are shown as dashed lines.

Table 1
The Referred Pharmacokinetic Parameters and ke0 for Predicting Effect Site Concentrations
|
Parameter |
T1% |
TOF |
|
Roc |
Cis |
Roc |
Cis |
|
V1 (L) |
4.04 |
0.035 × WT |
exp(−0.00143 × [CrCl − 118.90]) × 4.73 × (WT/70) |
0.035 × WT |
|
V2 (L) |
5.34 |
0.083 × WT |
exp(0.00613 × [age − 43.00]) × 6.76 × (WT/70) |
0.083 × WT |
|
V3 (L) |
4.93 |
|
|
|
|
CL1 (L/min) |
0.26 |
|
(1 − 0.00678 × (age − 43.00)) × 0.269 × (WT/70)0.75
|
|
|
CL2 (L/min) |
0.36 |
|
0.279 × (WT/70)0.75
|
|
|
CL3 (L/min) |
0000.04 |
|
|
|
|
k10 (/min) |
|
0.053 |
|
0.053 |
|
k12 (/min) |
|
0.185 |
|
0.185 |
|
k21 (/min) |
|
0.049 |
|
0.049 |
|
ke0 (/min) |
|
0.054 |
|
0.0613 |
Table 2
Parameter Estimates that Resulted from Modeling
|
Model |
Parameter |
T1% |
TOF |
|
Estimate (RSE, %) |
CI (lower, upper) |
Estimate (RSE, %) |
CI (lower, upper) |
|
Greco |
Ce50,r (ng/ml) |
1180 (4.5) |
(1075, 1285) |
974 (4) |
(898, 1050) |
|
Ce50,c (ng/ml) |
464 (5.3) |
(416, 512) |
421 (5.1) |
(379, 463) |
|
E0
|
95.6 (1.4) |
(93, 98.2) |
96.1 (0.7) |
(94.7, 97.5) |
|
α |
1.12 (32.1) |
(0.41, 1.83) |
0.977 (31.9) |
(0.365, 1.59) |
|
γ |
5.36 (8.3) |
(4.52, 6.26) |
5.31 (6.8) |
(4.61, 6.01) |
|
Emax
|
0 |
|
0 |
|
|
Minto |
Ce50,r (ng/ml) |
1180 (4.5) |
(1075, 1285) |
976 (4) |
(899, 1053) |
|
Ce50,c(ng/ml) |
463 (5.4) |
(414, 512) |
420 (5.1) |
(378, 462) |
|
U0 |
95.5 (1.4) |
(92.9, 98.1) |
95.9 (0.7) |
(94.5, 97.3) |
|
β |
0.786 (23.8) |
(0.419, 1.153) |
0.715 (23.4) |
(0.387, 1.04) |
|
δ |
5.89 (7.9) |
(4.97, 6.81) |
5.76 (6.4) |
(5.04, 6.48) |
|
Umax |
0 |
|
0 |
|















