Interpretation of volume kinetics in terms of pharmacokinetic principles
Article information
Abstract
Volume kinetics is the pharmacokinetics of infusion fluids and describes the distribution and elimination of infused volume. Generally, pharmacokinetic parameters can be estimated by measuring the concentration of a drug. However, it is almost impossible to directly measure the concentration of fluids. Therefore, in volume kinetics, the disposition of fluids is indirectly quantified by measuring the hemoglobin concentration under the premise of no hemoglobin loss. If the hemoglobin concentration is repeatedly measured while administering the fluids, the dilution (relative change of the plasma volume) for each corresponding hemoglobin concentration can be obtained. The dilution is based on the concept of plasma volume expansion. The method of quantifying the drugs disposition with compartmental analysis has been equally applied to volume kinetics. The transfer of fluids between compartments is explained by first-order kinetics, and it is assumed that fluid is only removed from the central compartment. Population analysis can be used to identify covariates that can account for inter-individual variability in volume kinetic parameters. Body weight and mean blood pressure are well-known representative covariates of kinetic volume parameters. Using volume kinetic parameters, the volume expansion effects of crystalloid and colloid solutions can be understood more effectively, thereby facilitating appropriate fluid therapy. Although limitations exist in volume kinetics, its implications are important for clinicians when administering fluids.
Introduction
Maintenance of stable vital signs is crucial during surgery. In this context, anesthesiologists typically attempt to select an appropriate fluid type and administer the necessary amount to the patient. The quantification disposition of fluids administered to the body facilitates an efficient fluid administration. This process is similar to that used to describe the pharmacokinetics of intravenous drugs. Pharmacokinetic parameters can be estimated by measuring the concentration of a drug. However, it is almost impossible to directly measure the concentration of fluids. Therefore, the distribution and elimination of fluids are indirectly described by measuring endogenous substances that change as fluids are administered. Hemoglobin is primarily used as an endogenous tracer. An anesthesiologist named Robert G. Hahn established an analysis method for fluid volume kinetics [1]. The method of quantifying the disposition of drugs with compartmental analysis was equally applied to volume kinetics. Therefore, to obtain a comprehensive understanding of volume kinetics, it is important to understand the pharmacokinetics, which is the basis of the theory. Herein, the general yet fundamental concept of volume kinetics in terms of pharmacokinetic principles is presented.
Pharmacokinetic principles for understanding volume kinetics
Because general anesthesia is performed using various hypnotics and analgesics, anesthetic pharmacology can be considered as a basic subject for anesthesiologists. The basis for understanding pharmacology is the pharmacokinetic equation. The pharmacokinetic equation quantitatively evaluates drug transfer in the body and can be easily induced based on a few principles. In mammillary compartmental models, the kinetics of drug transfer between compartments were initially determined. Subsequently, linear differential equations were constructed based on kinetics. The Laplace transforms of these differential equations can be used to derive functions to calculate drug amounts in the central or peripheral compartments. In addition, the inverse Laplace transforms of these functions are used to obtain the pharmacokinetic equations in the time domain.
Kinetics of drugs
Pharmacokinetics is typically referred to as the ADME of a drug, which is acronym for absorption, distribution, metabolism, and excretion. Metabolism and excretion are known as elimination, and distribution and elimination are known as disposition. Kinetics refers to the process by which drugs are transferred to the body. Depending on the type of kinetics involved during absorption, distribution, and elimination, the differential equation describing the change in drug amount in the pharmacokinetic compartment varies, as well as the pharmacokinetic equation derived from it. Drug kinetics can be categorized into zero- and first-order kinetics. Zero-order kinetics are described when a fixed amount of a drug is consistently eliminated per time unit. Suppose that 100 mg of a drug exists in the body of an individual, and this drug follows the zero-order kinetics but its amount reduces by 10 mg per hour. Therefore, 90 mg of the drug will remain in the body of the individual after 1 h, 80 mg after 2 h, and 70 mg after 3 h (Fig. 1A). Because the volume of distribution for each drug is considered to be constant, the concentration is obtained by dividing the drug amount by the distribution volume. Therefore, the relationship between time and drug amount can be considered the same as that between time and concentration. Zero-order kinetics are simple and linear; however, drugs lost through zero-order kinetics are not common. In general, most drugs are lost through first-order kinetics. First-order kinetics refers to the loss (or inflow) of drugs per time unit by a certain fraction of X (t), which is the amount of drug remaining in the body. If the drug is lost, then the sign of rate of change for the drug amount will be negative; conversely, if the drug is introduced, then the sign will be positive. For instance, assume that 100 mg of a drug exists in the body of an individual, and 20% of the drug is lost per hour. After 1 h, 80 (= 100 − 100 × 0.2) mg of the drug will remain in the body, 64 (= 80 − 80 × 0.2) mg after 2 h, and 51.2 (= 64 − 64 × 0.2) mg after 3 h. This can be illustrated by an exponential curve, as shown in Fig. 1B. A mathematical understanding of the exponential decrease in first-order kinetics is important. The loss of drugs following first-order kinetics can be expressed as a differential equation as follows:

Zero-order (A) and first-order (B) kinetics. X: amount of drug, t: time in h, X0 = 100 mg, k: elimination rate constant (mg/h for zero-order kinetics and 1/h for first-order kinetics).
Applying the Laplace transform to this equation yields
The inverse Laplace transformation of this equation yields a drug amount function over time, as follows:
where e-kt refers to the fraction of the initial amount X (0) of the drug remaining in the body after the drug was removed by first-order kinetics during time t, and has a value between 0 and 1. Additionally, the disposition of fluids in the body can be explained by first-order kinetics.
Mammillary compartmental model
Compartmental analysis is an analysis method that partitions the body into several compartments and quantifies the transfer of drugs between compartments. Among the compartmental models, the mammary model is primarily used to estimate the pharmacokinetic parameters of drugs. In the mammillary compartmental model, the central compartment is related to all other peripheral compartments, but no relationship exists among the latter. In addition, it is assumed that the transfer of drugs between the central and peripheral compartments is based on first-order kinetics. Furthermore, it is assumed that the drug is only removed from the central compartment. For example, a two-compartment mammillary pharmacokinetic model can be expressed as shown in Fig. 2. The differential equation for the change in drug amount by compartment is as follows:

Two-compartment mammillary pharmacokinetic model. I: input, kij: micro-rate constant from compartment i to compartment j, Vi: volume of distribution of compartment i. Here, i = 1, 2.
These differential equations are used in the same structural model to estimate the volume kinetic parameters. In Fig. 2, the pharmacokinetic parameters are expressed in the micro-rate constant domain (V1, k10, k12, k21). However, they can be expressed in terms of volume and clearance domain (V1 volume of distribution in the central compartment; V2 volume of distribution in the peripheral compartment; Cl, metabolic clearance; Q, inter-compartmental clearance). The relationship between the two domains can be described as follows:
In other words, if the pharmacokinetic parameters of one domain are estimated from the time-concentration curve, they can be converted to those of the other domain.
Population analysis
It is typically observed that different effects are exhibited in different individuals, even when the same weight-based dose was administered. This is owing to variabilities in pharmacokinetics and pharmacodynamics from one person to another. These variabilities may be due to a person’s specific characteristics (covariates). For example, these variabilities can occur because of weight, height, age, sex, race, and genetic variations. Population analysis is a method that can explain the inter-individual variability in pharmacokinetics and pharmacodynamics by mathematically connecting patient-specific covariates for each pharmacokinetic and pharmacodynamic parameter [2]. Unlike the standard two-stage method, which analyzes individual time–concentration curves separately, all individuals are analyzed at once to identify the characteristics that can be associated with the pharmacokinetic and pharmacodynamic parameters. Several software programs can be used to perform population analysis; however, the first and most representative is nonlinear mixed-effects modeling (NONMEM), created by Lewis B. Sheiner (physician) and Stuart L. Beal (statistician) of the University of San Francisco [3]. NONMEM is also the name of a standard software (ICON Development Solutions, Ireland) for population analysis. Fig. 3 shows the basic concept of population pharmacokinetic and pharmacodynamic analyses using NONMEM. In the mixed-effects model, a pharmacokinetic parameter is estimated by dividing mixed-effects by a fixed-effect parameter that does not change from person to person (θ in NONMEM) and a random-effect parameter between individuals (η in NONMEM). Herein, the random-effect parameter between subjects describes the random inter-individual variability of the pharmacokinetic parameters. This random variability between individuals exhibits a normal distribution with a mean of 0 and a variance of ω2, and it is a biologically natural phenomenon. In the population analysis, the part that can be explained by the patient’s characteristics (covariate) among the random inter-individual variability of the pharmacokinetic parameter is mathematically linked to the fixed-effect parameter. This is the essence of population analysis. Hence, the control stream of NONMEM is written as follows, using V1 (volume of distribution in the central compartment) as an example.
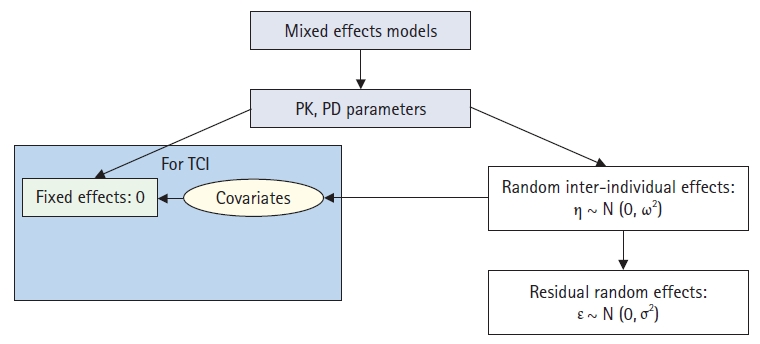
Concepts of population analysis using nonlinear mixed-effects modeling. PK: pharmacokinetics, PD: pharmacodynamics, TCI: target-controlled infusion.
TV1 = THETA(1)
V1 = TV1*EXP(ETA(1)),
where TV1 is a representative value of V1 (typical value, a typical human or population average value with zero variation between random individuals), and in this case, THETA(1). ETA(1) is the random effect parameter between individuals in V1. In other words, THETA(1) is connected by an exponential function with ETA(1). Additionally, they can be connected by multiplication or addition, and the one that best describes the data will be selected. Suppose that part of ETA(1) is described by the patient’s weight; in this case, the NONMEM control stream can be changed as follows:
TV1 = THETA(1) + THETA(2)*WT; WT = weight
When a pharmacokinetic model involving the equation above is incorporated into the target-controlled infusion system, the dose can vary based on weight [4,5]. Previously, in the field of volume kinetics, parameters were primarily estimated using MATLAB (Mathworks, Inc., USA), but population analysis has been primarily used since 2016 [6–9].
Calculation of plasma volume expansion caused by fluid administration using hemoglobin
If blood volume is defined as the volume of hemoglobin distribution, then hemoglobin can be used as an endogenous tracer to analyze the volume expansion of a fluid space. In this regard, the following two assumptions should be applied: (i) no loss of red blood cells; (ii) the hemoglobin concentration decreases as the plasma volume expands. Dr. Robert G. Hahn introduced a new method to calculate plasma volume expansion using hemoglobin in 1997 [1], and the effectiveness of this method was confirmed in clinical trials participated by healthy volunteers [10,11]. The plasma volume (Vp) at any time t after the start of intravenous infusion can be expressed as follows, based on the hematocrit (Hct).
where Vb(t) is the blood volume at any time t. Assuming that the volume of erythrocytes is constant during the observation time, then the volume of erythrocytes at t = 0 before intravenous infusion is equivalent to the volume of erythrocytes at any time t after intravenous infusion.
However, if bleeding occurs, Equation 7 does not hold. In other words, the amount of hemoglobin at t = 0 before intravenous infusion and the amount of hemoglobin at any time t after intravenous infusion will be the same. The hemoglobin level is calculated by multiplying the hemoglobin concentration and blood volume as follows:
Using Equations 6 and 8, the following equation can be derived.
If the amount of administered fluid is set as Ap, then Ap at any time t, i.e., Ap(t), during an intravenous infusion can be described as follows:
The relative change in the plasma volume induced by fluid infusion can be expressed as shown in Equation 11.
where Dp is dimensionless and is referred to as plasma dilution. Substituting Equation (10) into Equation 11 yields
The longer the administration of the fluid, the greater are Vp(t) and Dp(t), and this is equivalent to an increase in plasma volume due to the fluid administered. Substituting Equation (6) into Equation 12 yields
Substituting Equation 9 into Equation 13 yields
Combining Equations 7 and 8 yield the following:
Substituting Equation 15 into Equation 14 yields
If the hemoglobin concentration is repeatedly measured while administering the fluids, the degree of plasma volume dilution for each corresponding hemoglobin concentration can be obtained (Fig. 4). The degree of plasma volume dilution is the same as that of plasma volume expansion.

Changes in hemoglobin (A) and plasma dilution (B) caused by fluid administration. Male volunteer received 40 ml/kg Ringer’s lactate solution over 1 h. Dilution was calculated as follows:
where CHb(0) and Hct(0) are the hemoglobin concentration and hematocrit measured prior to the administration of Ringer’s lactate solution, respectively; CHb(t) is the hemoglobin concentration measured at any time t.
Structure model for volume kinetics
In volume kinetics, a mammillary compartment model is used to quantify fluid disposition. Table 1 shows a comparison of the similarities and differences between traditional pharmacokinetic and volume kinetic expressions.

Basic Similarities and Differences between Traditional Pharmacokinetic and Volume Kinetic Expressions
One-volume model
The one-compartment model is suitable for quantifying the disposition of fluids that are predominantly distributed in blood vessels, such as colloids [12,13]. When the last hemoglobin measurement time is insufficient to capture the elimination phase, then crystalloids can be explained using the one-volume model. A schematic diagram of the one-volume model is shown in Fig. 5. Based on this figure, the differential equation in the one-volume model can be described as follows:
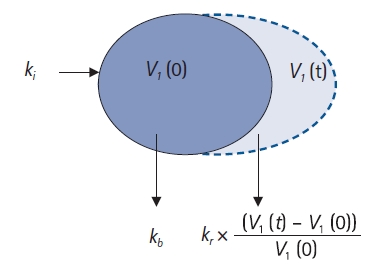
One-volume model. ki: infusion rate of the fluid (ml/min), kb: basal elimination reflecting ongoing losses of water due to respiration, sweating, and basal renal filtration (ml/min), kr: renal clearance (ml/min), V1(0): plasma volume at t = 0 before intravenous infusion (ml), V1(t): plasma volume at any time t after intravenous infusion (ml).
In this study, basal elimination (kb) was not estimated and was set as a fixed value. In general, kb is 0.5–1.5 ml/min in adults [14]. Robert G. Hahn often set it to 0.8 or 1.0 ml/min for modeling [10,11]. If the data are fitted to the model, then the estimated value of renal clearance (kr) will exceed 100 ml/min; therefore, even if kb is fixed to a specific value in the range of 0.5–1.5 ml/min, the actual estimated value will not be affected significantly.
Two-volume model
The two-volume model is widely used in volume kinetics, and it can be used to effectively explain the plasma dilution-time data observed when crystalloids are administered [6,15]. A schematic diagram of the structural two-volume model is shown in Fig. 6. Based on this figure, the differential equation for the two-volume model can be written as follows:
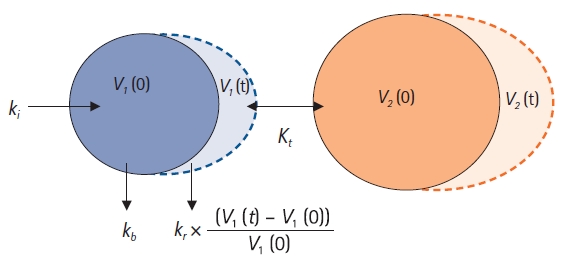
Two-volume model. ki: infusion rate of the fluid (ml/min), kb: basal elimination reflecting ongoing losses of water due to respiration, sweating, and basal renal filtration (ml/min), kr: renal clearance (ml/min), V1(0): plasma volume at t = 0 before intravenous infusion (ml), V1(t): plasma volume at any time t after intravenous infusion (ml), V2(0): peripheral volume at t = 0 before intravenous infusion (ml), V2(t): peripheral volume at any time t after intravenous infusion (ml), kt: distributional clearance (ml/min).
In pharmacokinetics, the transfer of drugs between the central and peripheral compartments is classified into k12 and k21; however, in volume kinetics, it is estimated as kt. This can be understood by recalling that the observed value in volume kinetics is the plasma dilution measured based on the hemoglobin concentration. Because hemoglobin exists only in blood vessels, it cannot move to the peripheral compartment, and it may be impossible to estimate the rate at which fluid propagates from the peripheral compartment to the central compartment or is cleared through the lymphatic system. In addition, owing to the nature of crystalloids, the rate of transfer between the central and peripheral compartments will not differ significantly. Moreover, it is beneficial to reduce the number of parameters to be estimated to ensure model stability (parsimonism). In some studies, k12 and k21 were estimated separately using the two-volume model [6-9]. The objective function value of a model can be reduced significantly by distinguishing the two parameters; however, this often causes model instability. Considering these characteristics of volume kinetics, it is almost impossible to explain the plasma dilution-time data of crystalloids using a three-volume model. The NONMEM control streams for one- and two-volume models are presented in the Appendix 1.
Calculation of renal clearance using urine volume
The fluid administered was primarily removed by renal clearance (kr). Because renal clearance is proportional to the plasma volume expansion, the following differential equation can be established:
where U(t) is the urine volume at time t. If the total urine volume (UTOT) is known during the entire observation time T, then kr and kb can be calculated as follows:
As previously mentioned, kb is typically 0.5–1.5 ml/min in adults [14]. Herein, kr∙AUC(Dp) refers to the urine volume produced by intravenous infusion, and kb∙T the urine volume induced by basal elimination. However, in reality, renal clearance is controlled by a complex mechanism that involves various hormones such as antidiuretic hormone, renin-angiotensin, atriopeptin, aldosterone, and angiotensin II [14]. Moreover, specific cell receptors are involved, including baroreceptors and osmoreceptors that regulate salt and water homeostasis [14]. Renal clearance can be obtained via two methods. The first is an estimation method from the structural model of volume kinetics, and the second is a calculation method based on the area under the time–dilution curve for the central compartment divided by the observed total urinary output [15]. The more accurate method is yet to be determined. However, it is reasonable to estimate kr from the same dataset with other volume kinetic parameters.
Covariates describing inter-individual variabilities of volume kinetic parameters
In pharmacokinetics, the inter-individual variability in the distribution volume is well explained by body weight, and the clearance is primarily explained by body weight or age [5,16,17]. Similar results have been reported in previous studies pertaining to the volume kinetics (Table 2). Body weight is a significant covariate for the distribution volume in the central compartment [7,15]; furthermore, it is physiologically reasonable that the greater the weight, the larger is the plasma volume. Renal clearance deteriorates with age [7], i.e., a natural aging process. An interesting fact is that the mean blood pressure is a significant covariate in renal clearance [7,15]. A positive correlation exists between mean blood pressure and renal clearance; this implies that the lower the mean blood pressure is clinically, the more severe is fluid retention in the body. This can be observed more clearly when simulated using a volume kinetics model [15]. The simulated volume expansion of the central and peripheral compartments in a hypothetical patient who was administered 10 ml/kg of Ringer’s lactate solution over 15 min followed by a rate of 8 ml/kg/h for 165 min is presented in Fig. 7. In patients of the same weight, it was observed that the lower the average blood pressure, the greater was the fluid retention in the interstitium. In clinical practice, fluid is generally administered in consideration of body weight, but relatively rarely in consideration of mean blood pressure. When blood pressure decreases, more fluids are typically administered. In this case, if the blood pressure does not recover as expected, the fluids administered will continue to accumulate in the interstitium.
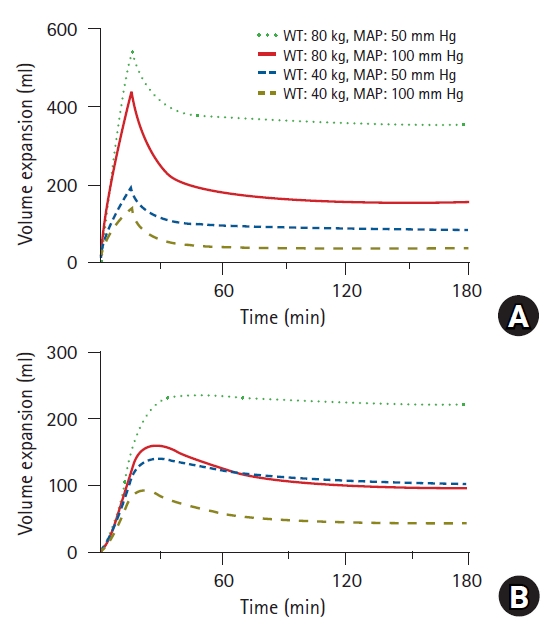
Simulated volume expansions of central (A) and peripheral (B) compartments in hypothetical patient receiving 10 ml/kg of Ringer’s lactate solution over 15 min followed by a rate of 8 ml/kg/h for 165 min. Four different cases were simulated based on weight (40 vs. 80 kg) and mean arterial pressure (50 vs. 100 mmHg). WT: weight, MAP: mean arterial pressure.
Clinical application of volume kinetics
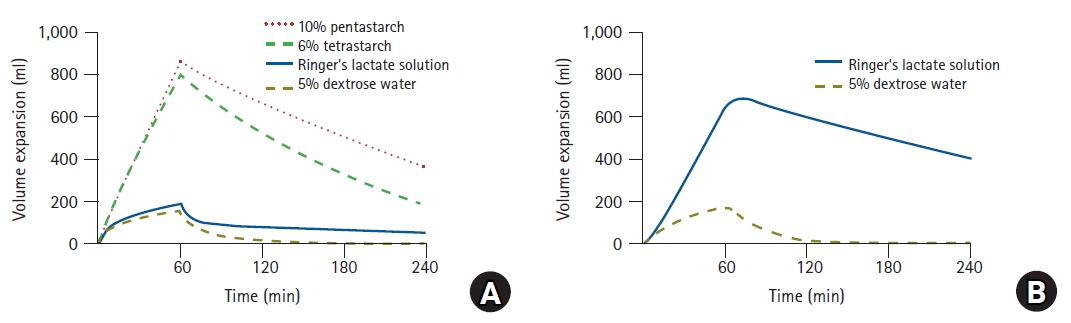
Understanding volume kinetics enables the distribution of fluids administered to the body to be described quantitatively. In a recent study, 12 male volunteers were randomly assigned to four groups, and each group received four fluid solutions in specified sequences, separated by 1-week intervals to avoid any carryover effects [13]. The volunteers received 1,000 ml of 6% tetrastarch (hydroxyethyl starch, HES 130/0.4; VOLULYTE, Fresenius Kabi AG, Germany), 1,000 ml of 10% pentastarch (HES 250/0.45; PENTASPAN, Jeil Pharmaceutical Co., Ltd., Korea), 40 ml/kg of Ringer’s lactate solution (JW Pharmaceutical Co., Ltd., Korea), and 20 ml/kg of 5% dextrose water (JW Pharmaceutical Co., Ltd., Korea) for 60 min. Changes in plasma dilution induced by the administration of crystalloids and colloids were described effectively using two- and one-volume models, respectively [13]. Volume expansion effects can be easily understood by performing simulations based on the fluid dynamics parameters of these crystalloids and colloids (Fig. 8) [13]. When the same volume was administered, the volume expansion effects of colloids were approximately four times higher than those of crystalloids by the time when the infusion was terminated. This can be interpreted as a validation of volume kinetics, in that a suggested theory (a crystalloid solution should have 1/4th the volume-expanding capacity of the colloid solution [18]) was proven through a scientific method. In addition, in the case of Ringer’s lactate solution, the simulation results show that only approximately 20% of the administered volume was present in the blood vessel at the end of the fluid administration, whereas approximately 70% propagated to the interstitium. Some studies indicated results that differed slightly from the simulation results [9,19,20]. However, the abovementioned approach may be beneficial in maintaining euvolemia to maintain stable hemodynamics during general anesthesia. The concentration and molecular weight of HES affect the volume expansion effect [21]. In the simulation study, 10% pentastarch demonstrated a long-lasting volume expansion compared with 6% tetrastarch [13]. This is because the renal clearance of 6% tetrastarch was greater than that of 10% pentastarch. Similarly, a previous study showed that 6% HES indicated a greater renal clearance than 10% HES solution [22]. As such, using volume kinetics enables the effect of volume expansion between HESs to be compared indirectly without directly measuring the plasma volume.
Limitations of fluid kinetics
Although fluid kinetics is a favorable methodology for quantifying the disposition of fluids, it has some limitations. First, it cannot explain the hemoconcentration observed in clinical practice. Hemoconcentration can be observed in patients undergoing restrictive fluid management [15]. This is because fluid is administered at the minimum amount required, and the urine output is relatively high. When hemoconcentration occurs, the value of plasma dilution is negative (Fig. 9A) [15]. The structural model of volume kinetics evaluates the volume expansion induced by fluid administration compared with the baseline, and the reduction from the initial volume is structurally unpredictable [15]. Therefore, even for the observed value with a negative dilution, the model will predict a positive value (Fig. 9B) [15]. Second, it fails to account for the transfer of fluids through the lymphatic system in the interstitium. As mentioned earlier, because the increase in plasma volume due to the administration of fluids is indirectly quantified by measuring the hemoglobin concentration, the transfer of fluids in the interstitium without hemoglobin cannot be structurally explained. Hence, it is difficult to estimate the elimination clearance (k20) removed from the peripheral compartment without passing through the central compartment. In this regard, a previous study that explained the disposition of Ringer’s lactate solution based on a three-volume model is difficult to understand [23].
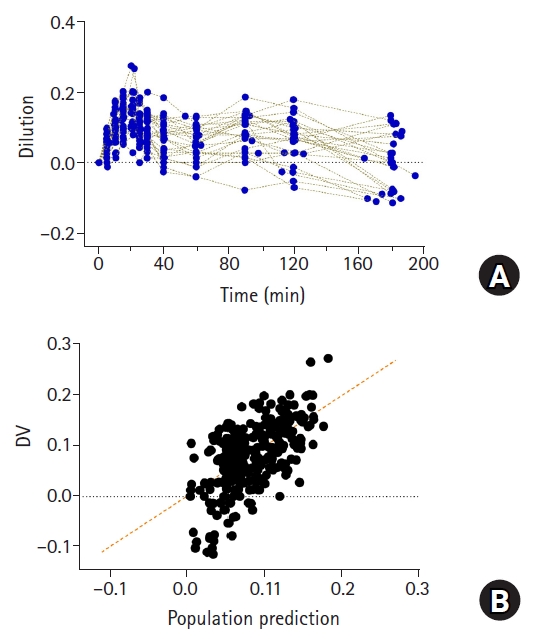
Plasma dilution (A) in 27 patients undergoing open gastrectomy. Patients were administered with 1,000 ml of Ringer’s lactate solution for 20 min, followed by continuous infusion at 6 ml/kg/h until time of last blood collection for volume kinetic analysis. Observed values (plasma dilutions) and population predicted values by volume kinetic model (B). Orange dashed line represents line of identity.
Conclusion
Volume kinetics is an effective method for quantitatively explaining the distribution and elimination of fluids administered to the body. The quantification of the disposition of drugs via compartmental analysis was applied to volume kinetics. The transfer of fluids between compartments was explained via first-order kinetics, and it was assumed that fluid was removed only in the central compartment. Volume expansion induced by the administration of fluids was indirectly evaluated by measuring the decrease in hemoglobin concentration. Using the volume kinetic parameters, the volume expansion effects of crystalloid and colloid solutions can be understood more effectively, thereby facilitating fluid therapy. Dr. Hahn’s research team has been conducting extensive research pertaining to volume kinetics. Nonetheless, further research can be pursued. Owing to the limitations of the structural model of fluid kinetics, it cannot reflect the clinical situation of all patients. However, even if the current method is used, it can provide reasonably meaningful implications to clinicians when administering fluids. Researchers should consider the patient group, type of infusion solution to be selected, and type of covariate to be added to achieve clinical significance. It is hoped that this review will facilitate research pertaining to volume kinetics.
Acknowledgements
I am deeply grateful to Dr. Robert G. Hahn for pioneering the quantification of the disposition of crystalloid and colloid solutions using a methodology known as volume kinetics. This work was supported by the Korea Medical Device Development Fund grant funded by the Korea government (the Ministry of Science and ICT, the Ministry of Trade, Industry and Energy, the Ministry of Health & Welfare, the Ministry of Food and Drug Safety) (Project Number: KMDF_PR_20200901_0031, 202011B25-01).
Notes
Conflicts of Interest
No potential conflict of interest relevant to this article was reported.