Alternatives to P value: confidence interval and effect size
Article information
Abstract
The previous articles of the Statistical Round in the Korean Journal of Anesthesiology posed a strong enquiry on the issue of null hypothesis significance testing (NHST). P values lie at the core of NHST and are used to classify all treatments into two groups: "has a significant effect" or "does not have a significant effect." NHST is frequently criticized for its misinterpretation of relationships and limitations in assessing practical importance. It has now provoked criticism for its limited use in merely separating treatments that "have a significant effect" from others that do not. Effect sizes and CIs expand the approach to statistical thinking. These attractive estimates facilitate authors and readers to discriminate between a multitude of treatment effects. Through this article, I have illustrated the concept and estimating principles of effect sizes and CIs.
Introduction
The leading scientific journals, including the Korean Journal of Anesthesiology (KJA) are claiming that P value-dependent decision and description have spoiled scientific thinking. Null hypothesis significant testing (NHST) is deemed to be a core of statistical inference method that verifies an established null hypothesis according to the given significance level. The most critical problem of NHST is to provide a simple and dichotomous decision in terms of a "yes" or a "no" [1]. This simplified interpretation produces an unsubstantiated expectation; the treatment applied by a researcher could have a sufficient effect in practice without the need to understand complex statistical inference procedures. In the real world, no disease or disastrous situation may be instantaneously overcome through a specific treatment. That is, the effect of a treatment should not be measured in terms of a simple "yes" or "no," but in terms of a scale. It is unscientific to assert that the statistical results are significantly "yes" or "no" with a predetermined error rate.
Statistics always begins with an inference, which carries uncertainty. In fact, statistical inferences produce results that indicate the probability of an impossible event in the real word. With this assumption, if you were to interpret the statistical results based solely on P values, you should explain the treatment effect to your patients as follows: "This treatment has a concrete effect with 95% probability. I hope that you will fall within that 95%." Alternatively, for patients who experience only a small improvement with the treatment, it is hard to claim that, "You are lucky! You are among the 95%!" The NHST results do not indicate the magnitude of the treatment effect nor the precision of measurement [2]. Treatment effects of specific medication cannot be categorically assessed into "yes" or "no" decisions. Instead, statistical results should clearly describe the magnitude of expected effects from the treatment. By using CI and effect size (ES), it is possible to explain the statistical results at some length.
This article contains the meanings of CI and ES, as well as the methods to compute and to interpret the computed CI and ES. The aim of this article is to provide readers with knowledge of the descriptions of statistical results using CIs and ESs, beyond the P values. Although this article does not cover all available ESs, it contains many equations. I hope that readers are able to understand and apply these equations to compute estimates, which may not be calculated automatically by statistical software.
Confidence Intervals
A 95% CI of the mean calculated from a sample implies that if the samples originate from the same population with the same extraction method, 95% of their CI ranges would include the population mean. For example, when we calculate 95% CI of the mean from our data and repeat the same experiment a hundred times, of the one hundred 95% CIs so computed from the data, 95 of them would include the population mean. This differs from the explanation that a 95% CI of the mean calculated from a single sample includes the population mean with a probability of 95%. We can ascertain that the latter interpretation is wrong from the estimating process for CIs. The 95% CI of the mean of a normally distributed sample is calculated using the point estimate of the mean and its standard error of the mean (SEM), and the probability values of both ends corresponded to 2.5% each. That is, CI of the mean is calculated from a sampling distribution, which definitely differs from the population [3]. Hence, "a 95% CI includes the population mean with a 95% probability" is an incorrect interpretation. The right interpretation is that "the population mean would be included within the ranges of 95% of the CIs of the mean calculated from repeatedly sampled data with a 95% probability." At first glance, this seems to be similar to NHST, which uses P values for interpretation. However, by adding the 95% CI of the mean into the statistical results, we can obtain the magnitude of the treatment effect in addition to the "yes" or "no" response to the statistical significance of the treatment effect. Thus, if the 95% CI of the mean includes 0 or 95% CI of the ratio includes 1, the statistical result would be non-significant. This is the same as P > 0.05 in NHST at the 5% significance level.
The extended interpretation of 95% CI of the mean as a range estimate is that the same treatment could produce an effect within an estimated range as long as the statistical significance is maintained. The interpretation using CI as a range estimate is more consistent with statistical hypotheses compared to that using a P value of NHST. Statistical results using CIs rather than P values are more reliable as CIs indicate the expected size of the effect. Fig. 1 presents the changes in CIs and significance limits according to sample size, while keeping the mean and standard deviation (SD) constant. Based on the data, with an increase in sample size, the range of the CI became narrower while the limits of significance remained relatively unchanged. For statistical results with the same P value, the estimated CIs become narrower and the estimated effects could become more reliable with a larger sample size.
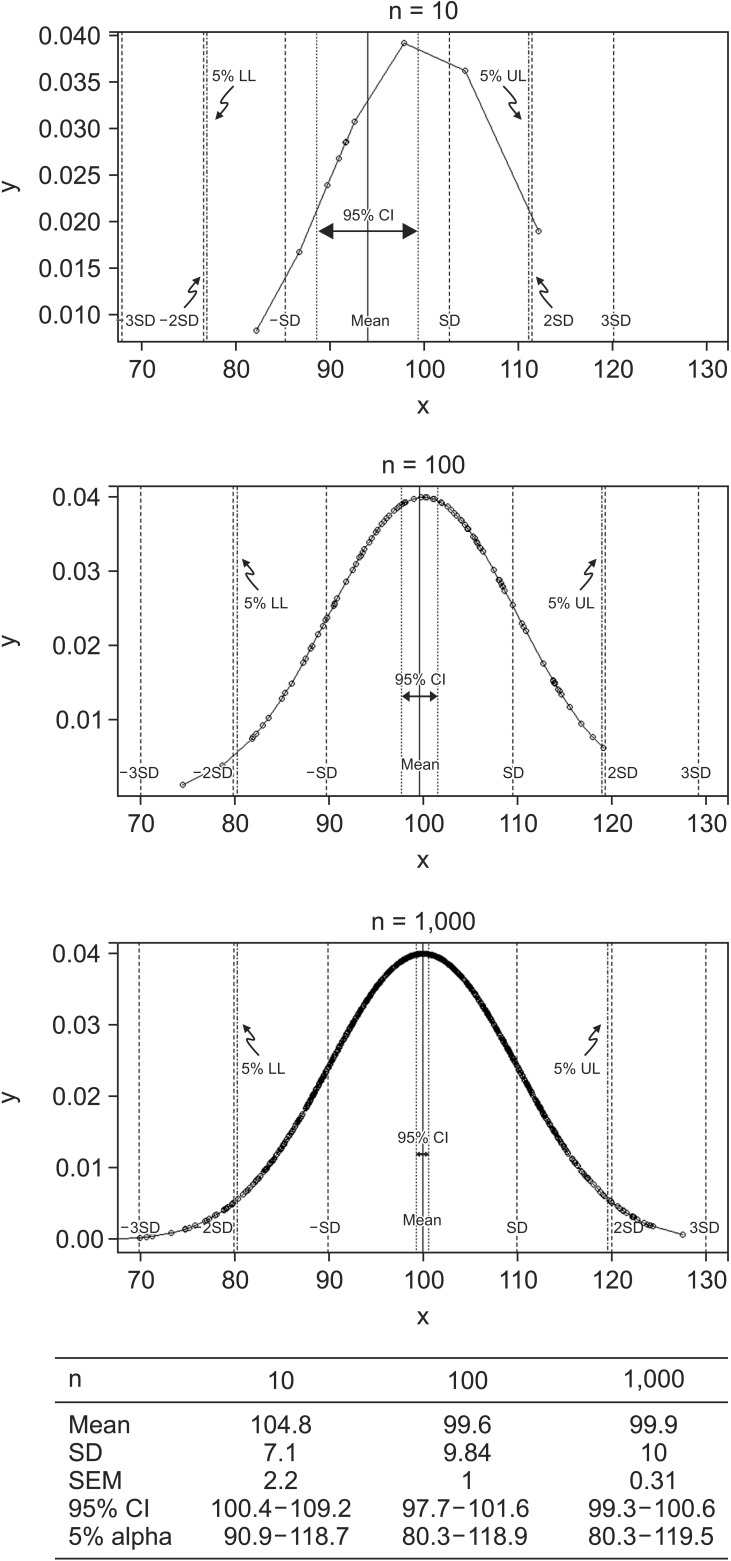
The changes in CI of the mean and alpha error values in accordance with sample size. All three data samples are randomly extracted using R system, under conditions of normal distribution with mean = 100, SD = 10. Each datum includes 10, 100, or 1000 samples. With the increase in sample size, the range of the 95% CI is considerably decreased from 8.8 for n = 10, 3.9 for n = 100 to 1.3 for n = 1000. The limits of 95% probability (5% alpha error limits) remains relatively unchanged as all three data samples were originated with the same mean and SD. This phenomenon implies that increase in sample size results in a more precise statistical inference (narrower CI) as well as increased statistical power. Critical values for alpha error probability are not much affected by increased sample size. These imaginary data are presented under the assumption of normal distribution with similar dispersions. SD: standard deviation, SEM: standard error of the mean.
For a continuous variable that is normally distributed, CI for a population mean may be calculated using the z critical values.
(α: confidence level, SEM: standard error of the mean, zα/2: z critical value at confidence level of α, corresponding to two tailed areas of α)
When comparing two normally distributed population means, it is useful to use CIs.
If two groups with small sample sizes fulfill the equal variance assumption, CIs may be calculated using t-statistics. In this situation, a pooled sample variance is applied into the CI calculation process [34].
(X̄i, si, ni: Mean, SD, and sample size of group i,
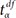 : t-critical value at confidence level of α and degree of freedom, df: degree of freedom)
: t-critical value at confidence level of α and degree of freedom, df: degree of freedom)
Theoretically, the SD from the control group is the best estimate of SD of the population as the members of the control group are sampled from the population without any treatment. However, this presupposes that the control group has a very large sample size. Hence, it is often better to use a pooled variance to calculate effect size. The basic concept of pooled variance is the calculation of an average of both groups' SD. This is different from the SD of all the values across both groups. That is, the pooled estimate of variance reflects more sensitively the differences between means and SDs of the two groups. The only assumption made when using pooled SD estimates is that the two groups originate from the same population. The sole difference between the two groups is the presence or absence of treatment. The pooled estimate of variance should not be used in statistical inference when this assumption does not hold. If samples have small sample sizes but do not fulfill the equal variance assumption, then either the variances can be made similar using log transformations or we may consider non-parametric statistics.
A different estimation process called analysis of variance (ANOVA) should be used for comparisons between three or more groups. ANOVA is the method of comparing the variations resulting from a factor, which causes a change in the population, and level of factors. Doing so avoids the α inflation, which emerges when repetitive paired comparisons are made. CI based on mean and SD does not reflect the variations caused due to factor and level, making paired comparisons impossible. To overcome this limitation, ANOVA uses the mean square error (the sum of the squared error of each group divided by the degrees of freedom) to calculate the CIs of groups.
(X̄i: mean of group i, ni: sample size of group i,
 : critical value of the t-distribution for the probability α and degrees of freedom ni–1, MSE: mean square error)
: critical value of the t-distribution for the probability α and degrees of freedom ni–1, MSE: mean square error)
When the result of the ANOVA is significant, post hoc tests (multiple comparison tests) are usually performed to compare each pair of groups. There are two methods for post hoc tests: one is the method based on corrected significant levels (e.g., Tukey, Bonferroni, and Scheffé's methods) and the other is the method of comparing pairs of groups based on the range of means (e.g., Duncan and Student-Newman-Keuls methods). To calculate CIs, the former applies a different method from that explained above. In case of Tukey's method, CIs are calculated using studentized range or q distribution [5].
Effect Size
As mentioned above, results of NHST only inform us of statistical significance without providing any information on the magnitude of the treatment effect. While CIs certainly alleviate this problem to some extent, they do not provide a definite answer but only a range of possibility. To readers who want to obtain information about the treatment, it is not useful to describe the expected results as "significant" or to state that "among 100 trials, mean effect of the treatment could be encountered in 95 trials." The best method to resolve this issue is to use a standardized way of measuring the treatment effect. This is called the effect size [678]. The effect size ameliorates the discrepancies between measuring units and enables comparisons between the statistical results arising from different measuring methods and different measuring units.
There are many kinds of the effect sizes. The first one is proposed by Cohen [9]. Most prominently, Cohen's d is one of the acclaimed effect sizes, Pearson's correlation coefficient r, and odds ratio are also types of effect sizes.
Cohen's d – effect size for the mean difference
When comparing two independent groups from a continuous variable, the student's t-test is usually used. If the result of NHST is significant, the magnitude of difference between the two groups may be simply expressed in terms of the difference between the means of the two groups. However, simple mean difference may be affected by measuring methods, units, and scales. When we assume that the variances of these groups are the same (this is the statistical assumption of equal variance), the amount of variation can be used to standardize mean difference. This is Cohen's d, the standardized mean difference between two groups.
(X̄T, X̄C: Mean for treatment and control groups)
SD refers to the population variance, which is never known. Hence, instead of applying the population's SD, we must either estimate this from the control group or use pooled SD, which is the same as the one used for CI computations.
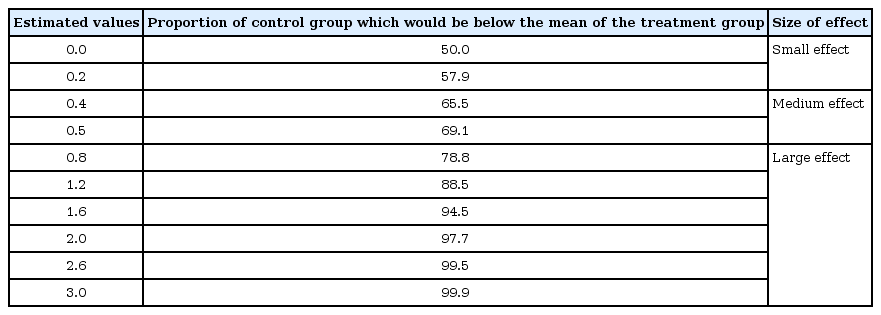
What is the exact meaning of effect size, especially Cohen's d? Cohen's d is the same as a "z-score" of a standard normal distribution. Using this score, Cohen's d can be converted into a scale of percentiles between two compared groups. For example, Cohen's d = 0.5 means that the mean of the treatment group is 0.5 SD above the mean of the control group. That is, 69% (a value of standard normal cumulative distribution function of 0.5) samples of the control group would be below the mean of the treatment group [4]. Although t statistic is exactly same with Cohen's d, we postulate that Cohen's d is calculated under the assumption of standard normal distribution. Thus, we can imagine the number of observations in the control group that are below the mean of the treatment group in terms of a percentile scale. Table 1 illustrates the expected percentiles at different Cohen's d values.
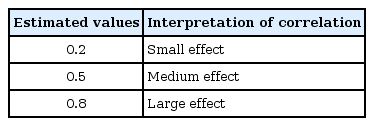
If we were to create a dummy variable to represent group assignment, which takes on a value of 0 for the control group and 1 for the treatment groups, this data could be analyzed using correlation tests. We may hypothesize that when a t-test result is significant, the correlation test results may also be significant. Based on this relationship, Cohen's d can be easily converted into correlation coefficient r [10]. The interpretation of effect size using r is called binomial effect size display (BESD) [11]. The main concept of BESD is that "r" is the representative value of the difference between two groups when grouping variables are converted into one dichotomy and observed values into another, such as being above or below a specific value like a mean [121314]. The interpretation of Pearson's r is also easy (Table 2) [15].
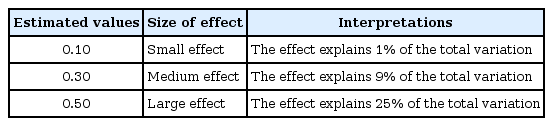
Another simple method of interpreting effect size is following the predetermined guide by Cohen (Table 1) [10]. However, this simple interpretation was criticized as it ignored the effectiveness of the treatment, which is not related to effect size [16]. For example, consider an inexpensive and safe medicine, which shows small improvements in sugar control in diabetes patients. The value of this medicine is somewhat large even though the effect size is small when we consider the improvements in the patients' economic and social conditions.
Confidence interval for Cohen's d
Unfortunately, effect size is not omnipotent. While it contains more information in comparison to P values, it is also an estimate, which is calculated from statistical inference. That is, an effect size that is estimated from a data of large sample size is likely to more accurate than one estimated from a data of small sample size. Hence, the concepts of confidence intervals may be applied to quantify the error imposed on an effect size. That is, a 95% confidence interval for effect size means a 5% alpha error level for effect size. The interpretation of the confidence interval for effect size is the same as that in the case of the CI of the mean. For all hypothetically sampled data from the same population and using the same sampling method, an effect size of population would fall within 95% of calculated 95% CIs for effect size of these data. If this 95% CI contains "0," it indicates "statistical non-significance." Providing the effect size (point estimate) and CI (the precision of effects) are essential to understand the magnitude of intended treatment effects.
Most statistical software do not support the calculation of the effect size and the corresponding CI. We need to understand the concepts behind the CI for effect size in order to manually calculate this CI using R system or other spreadsheet software. In the case of Cohen's d, Hedge and Olkin [17] provided a formula for estimating CI for effect size, subject to the condition of normal distribution.
95% CI for Cohen's d: [d − 1.96 × σ(d), d + 1.96 × σ(d)]
(Ni: the sample size of group i)
Confidence Interval for Pearson's r
Similar to other statistics, Pearson's r has its own sampling distribution. This distribution is similar to the normal distribution when the correlation is small, and incrementally changes into a negatively skewed distribution as the correlation increase. This unique distribution may be converted into a normal distribution by Fisher's r-to-z transformation [18]. Using the equation z = 0.5 log([1 + r] / [1 − r]), r-to-z transformation is possible, z follows the normal distribution with an 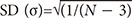 , where N is the number of pairs included in the correlation analysis. With this assumption, we first calculate a 95% CI of z and then convert this into r using the equation above.
, where N is the number of pairs included in the correlation analysis. With this assumption, we first calculate a 95% CI of z and then convert this into r using the equation above.
Variance-accounted-for effect size
The standardized mean difference is sufficient to compare the means of two groups. Apart from this, there are many other statistical inference methods and the effect size of these methods should be considered. When comparing three or more groups, the ANOVA is usually applied to compare the variations between groups. In the case of ANOVA, η2 is commonly used to represent effect size and is determined by the standardization of sum of squares, which are the representative values of data variability.
(SSB: sum of squares between groups, refers to the variability of the individual group means about the overall mean. SST: total sum of squares of the observations about the overall mean)
Fortunately, all parametric analyses include the correlation between groups and originate from a General Linear Model (GLM) including t-test, ANOVA, ANCOVA (Analysis of covariance), and MANOVA (multivariate analysis of variance) [18]. With respect to GLM, the same equation is used to calculate the Pearson r2 or regression coefficient R2 in multiple regression and these are considered the effect size of each method. These estimates are interpreted in a similar manner. With a treatment as an independent variable, 10% of the variability of the outcome can be explained when the effect size, η2, is 0.1 [19].
Corrected variance-accounted-for effect size
Furthermore, if the statistical analysis is related to Ordinary Least Squares (OLS), the effect size is estimated by a model fitting procedure. Effect size estimated by OLS such as multiple regression is more generalized when the sample data sufficiently reflects the population. However, this process is prone to naturally occurring bias, arising from inter- and intra-individual variations. These biases are more significant when the sample size is small, the number of measured variables is large, and the population effect size is small [12]. In this respect, the Ezekiel correction is assumed and is applied to both the Pearson r2 or R2 in multiple regression. The corrected effect size is termed corrected R squared (R2*).
(p: number of independent variables)
For the ANOVA statistic, Hays' ω2 is a corrected variance-accounted-for effect size, which can be calculated as follows [17].
(SSB, SST, MSW: sum of squares of between subject, total sum of squares, and mean square within subject, k: levels of predictor)
Effect sizes for contingency tables
Odds ratio (OR) and relative risk (RR) are good examples of effect sizes for 2 × 2 contingency table analyses. CIs of OR or RR can be estimated using the log standard error, which is computed using a type of Taylor series expansion called the Delta method [2021]. Based on the data characteristics, either OR or RR is applied and its corresponding CI can be estimated.
| Event (+) | Event (−) | |
|---|---|---|
| Treatment | a | b |
| Control | c | d |
(EF: error factor, calculated using standard error of log [OR])
Cohen's h is commonly used to compare two independent ratios or probabilities. This requires arcsine transformation, which is a reversed function of sine. Through this transformation, ratios or probabilities between 0 to 1 are transformed into negative and positive infinite values, which enables the calculation of binomial proportion CI of the dependent variable expressed with 0 and 1 [22]. Cohen's h can be calculated from the difference between two arcsine transformed ratios.
(p1, p2: two independent proportions)
Cohen's h represents the size of difference and is expressed either as directional h to indicate which ratio is bigger between two ratios, or as non-directional h to represent only the size of the difference through the absolute value of Cohen's h. Table 3 illustrates the interpretation of Cohen's h [23].
In the case of chi-square analysis, Φ(phi) coefficient is a good estimator of effect size for 2 × 2 contingency tables and reflects the magnitude of association between columns and rows.
(χ2: the chi-square statistic)
When the contingency table is larger than 2 × 2, Cramér's V is frequently used to explain the strength of association from chi-square analyses.
(k: the smaller number of rows or columns)
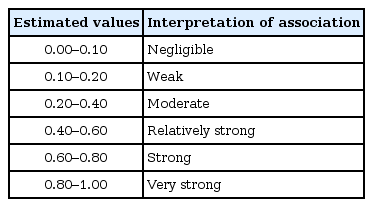
Interpretations of Φ and Cramér's V are illustrated in Table 4 [24].
Statistical reporting with effect sizes and confidence intervals
A standardized statistical reporting template containing the effect sizes and corresponding CIs is not yet established. Several articles report statistical results using the effect sizes and CIs; some authors describe these in great detail [25], others only state the effect sizes and CIs [26].
In order to report statistical results with the effect sizes and CIs, the statistical assumptions such as normality test and equal variance test should be exactly described in statistical methods explanation sections in addition to the estimates of representative value and degree of variations, the significance level of NHST, and the effect sizes used. An example of the statistical results report using Student's t-test is provided as per the following.
"A Student's t-test indicated that plasma concentrations (ng/dl) of propofol were significantly lower for group A (mean = 0.123, SD = 0.041, n = 66) than for group B (mean = 0.221, SD = 0.063, n = 67), a difference of −0.098 (95% CI: −0.116, −0.080), t(131) = −10.62, P < 0.001, Cohen's d = 1.84 (95% CI for Cohen's d: 1.44, 2.25)."
This seems more complex than the results using P values only; it highlights the quantitative difference between groups by interpreting the effect size. That is, the statistical result described above indicates that the mean of group B is significantly larger than the mean of group A by approximately 0.1 ng/dl, such that the effect of the treatment is large enough to increase the blood concentration in group B. This is a detailed description of the statistical report. However, if all statistical results are described in detail, the results section may appear unfocused. Simplified descriptions are also possible.
"The plasma concentrations (ng/dl) of propofol were significantly lower for group A (mean = 0.123, 95% CI: [0.113, 0.133]) than for group B (mean = 0.221, 95% CI: [0.206, 0.236]), P < 0.001, Cohen's d = 1.84)."
Either way, the explanation of the statistical significance and magnitude of difference should be provided.
Conclusion
The expression of statistical results with effect sizes and CIs provides a more comprehensive method of statistical results interpretation not only in terms of statistical significance but also the size of treatment effects. A significant P value cannot explain the latter even when the P value is as small as zero. Although the treatment effects cannot be classified into a dichotomous result, most articles determine their intended treatment effects to be significant or not significant with NHST. In such situations, the result with P = 0.51 or P = 0.49 was interpreted using terms such as "possibility," "trend," and so on. A solution to this problem is to use the effect size and CIs for the statistical results description. There are many equations and complex concepts for CIs and effect sizes, we should understand the exact meanings of these estimates and should use them appropriately when interpreting and describing statistical results. The results of a well-organized study contain statistical interpretations that cannot explained through the P values of NHST [1]. Unfortunately, the best method to replace NHST has not been discovered. As such, it is recommended that the effect size and its corresponding CI should also be included in order to enhance the statistical strength for the authors' interpretation.