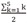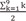Nonparametric statistical tests for the continuous data: the basic concept and the practical use
Article information
Abstract
Conventional statistical tests are usually called parametric tests. Parametric tests are used more frequently than nonparametric tests in many medical articles, because most of the medical researchers are familiar with and the statistical software packages strongly support parametric tests. Parametric tests require important assumption; assumption of normality which means that distribution of sample means is normally distributed. However, parametric test can be misleading when this assumption is not satisfied. In this circumstance, nonparametric tests are the alternative methods available, because they do not required the normality assumption. Nonparametric tests are the statistical methods based on signs and ranks. In this article, we will discuss about the basic concepts and practical use of nonparametric tests for the guide to the proper use.
Introduction
Statistical analysis is a universal method with which to assess the validity of a conclusion. It is one of the most important aspects of a medical paper. Statistical analysis grants meaning to otherwise meaningless series of numbers and allow researchers to draw conclusions from uncertain facts. Hence, it is a work of creation that breathes life into data. However, the inappropriate use of statistical techniques results in faulty conclusions, inducing errors and undermining the significance of the article. Moreover, medical researchers must pay more attention to acquiring statistical validity as evidence-based medicine has taken center stage on the medicine scene in these days. Recently, rapid advances in statistical analysis packages have opened doors to more convenient analyses. However, easier methods of performing statistical analyses, such as inputting data on software and simply pressing the "analysis" or "OK" button to compute the P value without understanding the basic concepts of statistics, have increased the risk of using incorrect statistical analysis methods or misinterpreting analytical results [1].
Several journals, including the Korean Journal of Anesthesiology, have been striving to identify and to reduce statistical errors overall in medical journals [2345]. As a result, a wide array of statistical errors has been found in many papers. This has further motivated the editors of each journal to enhance the quality of their journals by developing checklists or guidelines for authors and reviewers [6789] to reduce statistical errors. One of the most common statistical errors found in journals is the application of parametric statistical techniques to nonparametric data [45]. This is presumed to be due to the fact that medical researchers have had relatively few opportunities to use nonparametric statistical techniques as compared to parametric techniques because they have been trained mostly on parametric statistics, and many statistics software packages strongly support parametric statistical techniques. Therefore, the present paper seeks to boost our understanding of nonparametric statistical analysis by providing actual cases of the use of nonparametric statistical techniques, which have only been introduced rarely in the past.
The History of Nonparametric Statistical Analysis
John Arbuthnott, a Scottish mathematician and physician, was the first to introduce nonparametric analytical methods in 1710 [10]. He performed a statistical analysis similar to the sign test used today in his paper "An Argument for divine providence, taken from the constant regularity observ'd in the Births of both sexes." Nonparametric analysis was not used for a while after that paper, until Jacob Wolfowitz used the term "nonparametric" again in 1942 [11]. Then, in 1945, Frank Wilcoxon introduced a nonparametric analysis method using rank, which is the most commonly used method today [12]. In 1947, Henry Mann and his student Donald Ransom Whitney expanded on Wilcoxon's technique to develop a technique for comparing two groups of different number of samples [13]. In 1951, William Kruskal and Allen Wallis introduced a nonparametric test method to compare three or more groups using rank data [14]. Since then, several studies have reported that nonparametric analyses are just as efficient as parametric methods; it is known that the asymptotic relative efficiency of nonparametric statistical analysis, specifically Wilcoxon's signed rank test and the Mann-Whitney test, is 0.955 against the t-test when the data satisfies the assumption of normality [1516]. Ever since when Tukey developed a method to compute confidence intervals using a nonparametric method, nonparametric analysis was established as a commonly used analytical method in medical and natural science research [17].
The Basic Principle of Nonparametric Statistical Analysis
Traditional statistical methods, such as the t-test and analysis of variance, of the types that are widely used in medical research, require certain assumptions about the distribution of the population or sample. In particular, the assumption of normality, which specifies that the means of the sample group are normally distributed, and the assumption of equal variance, which specifies that the variances of the samples and of their corresponding population are equal, are two most basic prerequisites for parametric statistical analysis. Hence, parametric statistical analyses are conducted on the premise that the above assumptions are satisfied. However, if these assumptions are not satisfied, that is, if the distribution of the sample is skewed toward one side or the distribution is unknown due to the small sample size, parametric statistical techniques cannot be used. In such cases, nonparametric statistical techniques are excellent alternatives.
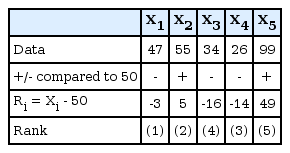
Nonparametric statistical analysis greatly differs from parametric statistical analysis in that it only uses + or - signs or the rank of data sizes instead of the original values of the data. In other words, nonparametric analysis focuses on the order of the data size rather than on the value of the data per se. For example, let's pretend that we have the following five data for a variable X.
After listing the data in the order of their sizes, each instance of data is ranked from one to five; the data with the lowest value (18) is ranked 1, and the data with the greatest value (99) is ranked 5. There are two data instances with values of 32, and these are accordingly given a rank of 2.5. Furthermore, the signs assigned to each data instance are a + for those values greater than the reference value and a − for those values less than the reference value. If we assign a reference value of 50 for these instances, there would only be one value greater than 50, resulting in one + and four − signs. While parametric analysis focuses on the difference in the means of the groups to be compared, nonparametric analysis focuses on the rank, thereby putting more emphasis differences of the median values than the mean.
As shown above, nonparametric analysis converts the original data in the order of size and only uses the rank or signs. Although this can result in a loss of information of the original data, nonparametric analysis has more statistical power than parametric analysis when the data are not normally distributed. In fact, as shown in the above example, one particular feature of nonparametric analysis is that it is minimally affected by extreme values because the size of the maximum value (99) does not affect the rank or the sign even if it is greater than 99.
Advantages and Disadvantages of Nonparametric Statistical Analysis
Nonparametric statistical techniques have the following advantages:
- There is less of a possibility to reach incorrect conclusions because assumptions about the population are unnecessary. In other words, this is a conservative method.
- It is more intuitive and does not require much statistical knowledge.
- Statistics are computed based on signs or ranks and thus are not greatly affected by outliers.
- This method can be used even for small samples.
On the other hand, nonparametric statistical techniques are associated with the following disadvantages:
- Actual differences in a population cannot be known because the distribution function cannot be stated.
- The information acquired from nonparametric methods is limited compared to that from parametric methods, and it is more difficult to interpret it.
- Compared to parametric methods, there are only a few analytical methods.
- The information in the data is not fully utilized.
- Computation becomes complicated for a large sample.
In summary, using nonparametric analysis methods reduces the risk of drawing incorrect conclusions because these methods do not make any assumptions about the population, whereas can have lower statistical power. In other words, nonparametric methods are "always valid, but not always efficient," while parametric methods are "always efficient, but not always valid." Therefore, parametric methods are recommended when they can in fact be used.
Types of Nonparametric Statistical Analyses
In this section, I explain the median test for one sample, a comparison of two paired samples, a comparison of two independent samples, and a comparison of three or more samples. The types of nonparametric analysis techniques and the corresponding parametric analysis techniques are delineated in Table 1.
Median test for one sample: the sign test and Wilcoxon's signed rank test
The sign test and Wilcoxon's signed rank test are used for median tests of one sample. These tests examine whether one instance of sample data is greater or smaller than the median (reference value).
Sign test
The sign test is the simplest test among all nonparametric tests regarding the location of a sample. This test examines the hypothesis about the median θ0 of a population, and it involves testing the null hypothesis H0: θ = θ0. If the observed value (Xi) is greater than the reference value (θ0), it is marked as +, and it is given a − sign if the observed value is smaller than the reference value, after which the number of + values is calculated. If there is an observed value in the sample that is equal to the reference value (θ0), the said observed value is eliminated from the sample. Accordingly, the size of the sample is then reduced to proceed with the sign test. The number of sample data instances given the + sign is denoted as 'B' and is referred to as the sign statistic. If the null hypothesis is true, the number of + signs and the number of − signs are equal. The sign test ignores the actual values of the data and only uses + or − signs. Therefore, it is useful when it is difficult to measure the values.
Wilcoxon's signed rank test
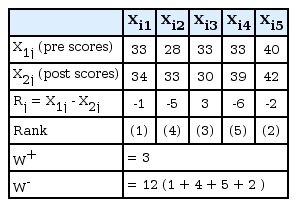
The sign test has one drawback in that it may lead to a loss of information because only + or − signs are used in the comparison of the given data with the reference value of θ0. In contrast, Wilcoxon's signed rank test not only examines the observed values in comparison with θ0 but also considers the relative sizes, thus mitigating the limitation of the sign test. Wilcoxon's signed rank test has more statistical power because it can reduce the loss of information that arises from only using signs. As in the sign test, if there is an observed value that is equal to the reference value θ0, this observed value is eliminated from the sample and the sample size is adjusted accordingly. Here, given a sample with five data points (Xi), as shown in Table 2, we test whether the median (θ0) of this sample is 50.
In this case, if we subtract θ0 from each data point (Ri = Xi - θ0), find the absolute value, and rank the values in increasing order, the resulting rank is equal to the value in the parenthesis in Table 2. With Wilcoxon's signed rank test, only the ranks with positive values are added as per the following equation:
Comparison of a paired sample: sign test and Wilcoxon's signed rank test
Sign test
In the previously described one-sample sign test, the given data was compared to the median value (θ0). The sign test for a paired sample compares the scores before and after treatment, with everything else identical to how the one-sample sign test is run. The sign test does not use ranks of the scores but only considers the number of + or − signs. Thus, it is rarely affected by extreme outliers. At the same time, it cannot utilize all of the information in the given data. Instead, it can only provide information about the direction of the difference between two samples, but not about the size of the difference between two samples.
Wilcoxon's signed rank test
This test is a nonparametric method of a paired t test. The only difference between this test and the previously described one-sample test is that the one-sample test compares the given data to the reference value (θ0), while the paired test compares the pre- and post-treatment scores. In the example with five paired data instances (Xij), as shown in Table 3, which shows scores before and after education, X1j refers to the pre-score of student j, and X2j refers to the post-score of student j. First, we calculate the change in the score before and after education (Rj = X1j - X2j). When Rj is listed in the order of its absolute values, the resulting rank is represented by the values within the parentheses in Table 3. Wilcoxon's signed rank test is then conducted by adding the number of + signs, as in the one-sample test. If the null hypothesis is true, the number of + signs and the number of − signs should be nearly equal.
The sign test is limited in that it cannot reflect the degree of change between paired scores. Wilcoxon's signed rank test has more statistical power than the sign test because it not only considers the direction of the change but also ranks the degree of change between the paired scores, providing more information for the analysis.
Comparison of two independent samples: Wilcoxon's rank sum test, the Mann-Whitney test, and the Kolmogorov-Smirnov test
Wilcoxon's rank sum test and Mann-Whitney test
Wilcoxon's rank sum test ranks all data points in order, calculates the rank sum of each sample, and compares the difference in the rank sums (Table 4). If two groups have similar scores, their rank sums will be similar; however, if the score of one group is higher or lower than that of the other group, the rank sums between the two groups will be farther apart.
On the other hand, the Mann-Whitney test compares all data xi belonging in the X group and all data yi belonging in the Y group and calculates the probability of xi being greater than yi: P(xi > yi). The null hypothesis states that P(xi > yi) = P(xi < yi) = ½, while the alternative hypothesis states that P(xi > yi) ≠ ½. The process of the Mann-Whitney test is illustrated in Table 5. Although the Mann-Whitney test and Wilcoxon's rank sum test differ somewhat in their calculation processes, they are widely considered equal methods because they use the same statistics.
Kolmogorov-Smirnov test (K-S test)
The K-S test is commonly used to examine the normality of a data set. However, it is originally a method that examines the cumulative distributions of two independent samples to examine whether the two samples are extracted from two populations with an equal distribution or the same population. If they were extracted from the same population, the shapes of their cumulative distributions would be equal. In contrast, if the two samples show different cumulative distributions, it can be assumed that they were extracted from different populations. Let's use the example in Table 6 for an actual analysis. First, we need to identify the distribution pattern of two samples in order to compare two independent samples. In Table 6, the range of the samples is 43 with a minimum value of 50 and a maximum value of 93. The statistical power of the K-S test is affected by the interval that is set. If the interval is too wide, the statistical power can be reduced due to a small number of intervals; similarly, if the interval is too narrow, the calculations become too complicated due to the excessive number of intervals. The data shown in Table 6 has a range of 43; hence, we will establish an interval range of 4 and set the number of intervals to 11. As shown in Table 6, a cumulative probability distribution table must be created for each interval (SX, SY), and the value with the greatest difference between the cumulative distributions of two variables (Max(SX - SY)) must be determined. This maximum difference is the test statistic. We compare this difference to the reference value to test the homogeneity of the two samples. The actual analysis process is described in Table 6.
Comparison of k independent samples: the Kruskal-Wallis test and the Jonckheere test
Kruskal-Wallis test
The Kruskal-Wallis test is a nonparametric technique with which to analyze the variance. In other words, it analyzes whether there is a difference in the median values of three or more independent samples. The Kruskal-Wallis test is similar to the Mann-Whitney test in that it ranks the original data values. That is, it collects all data instances from the samples and ranks them in increasing order. If two scores are equal, it uses the average of the two ranks to be given. The rank sums are then calculated and the Kruskal-Wallis test statistic (H) is calculated as per the following equation [14]:
Jonckheere test
Greater statistical power can be acquired if a rank alternative hypothesis is established using prior information. Let's think about a case in which we can predict the order of the effects of a treatment when increasing the degree of the treatment. For example, when we are evaluating the efficacy of an analgesic, we can predict that the effect will increase depending on the dosage, dividing the groups into a control group, a low-dosage group, and a high-dosage group. In this case, the null hypothesis H2 is better than the null hypothesis H1.
H0: [τ1 = τ2 = τ3]
H1: [τ1 , τ2, τ3 not all equal]
H2: [τ1 ≤ τ2 ≤ τ3, with at least strict inequality]
The Jonckheere test is a nonparametric technique that can be used to test such a rank alternative hypothesis [18].
The actual analysis process is described with illustration in Table 7.
Conclusion
Nonparametric tests and parametric tests: which should we use?
As there is more than one treatment modality for a disease, there is also more than one method of statistical analysis. Nonparametric analysis methods are clearly the correct choice when the assumption of normality is clearly violated; however, they are not always the top choice for cases with small sample sizes because they have less statistical power compared to parametric techniques and difficulties in calculating the "95% confidence interval," which assists the understanding of the readers. Parametric methods may lead to significant results in some cases, while nonparametric methods may result in more significant results in other cases. Whatever methods can be selected to support the researcher's arguments most powerfully and to help the reader's easy understandings, when parametric methods are selected, researchers should ensure that the required assumptions are all satisfied. If this is not the case, it is more valid to use nonparametric methods because they are "always valid, but not always efficient," while parametric methods are "always efficient, but not always valid".