Introduction
In a crossover study design, two or more treatments (e.g., drugs, procedures) are provided to subjects at different time periods, and the sequence of treatments is randomized for each subject. This design is applied to several fields such as bioequivalence clinical trials, and the simplest study design is a two-period, two-sequence crossover design (AB/BA design)
1). Subjects are randomly allocated to the AB or BA sequence
2) [
1,
2]. Subjects in the AB sequence receive treatment A in the first period, and after the effects of treatment A have subsided, they receive treatment B in the second period. The remaining subjects assigned to the BA sequence receive treatment B first and then treatment A (
Fig. 1). Therefore, the difference in treatments is derived from a within-subject comparison. On the other hand, in a parallel design, one subject receives only one treatment, therefore, the difference in treatments is derived from a between-subject comparison.
A crossover design has the following advantages. First, the treatment effect is compared within a subject since each subject serves as his or her own control. It removes the inter-subject variability from the comparison between groups and the effect of covariates
3) can be reduced [
3]. For this reason, the imbalance of allocation often seen in randomized controlled parallel studies are seldom seen in randomized controlled crossover designs. Second, the crossover design has high power and statistical efficiency. In other words, it is possible to obtain an estimate with the same level of accuracy as a parallel design, even with a smaller number of subjects [
1,
2,
4].
However, there are also limitations in the crossover design. First, the conditions of the subjects must be stable throughout the study. In other words, a case is inappropriate for a study if the disease status changes over time, such as an acute cure, or when symptoms disappear or are cured by treatment in the first period. Second, a washout period may be necessary until the effect of the first treatment subsides. Therefore, if a treatment drug has an extended half-life, it may be difficult to conduct a study with a crossover design. Third, there is a burden that all treatments are carried out on one subject, which often causes ethical problems. Fourth, the processing of dropped or missing data is more problematic than in a parallel design, and the statistical analysis is complex [
2,
4].
Based on these advantages and disadvantages, it will be helpful in planning and proceeding with an appropriate crossover design to fully understand the various factors encountered in its design and analysis process.
Standard 2 × 2 crossover design
The standard 2 × 2 crossover design is used to assess between two groups (test group A and control group B). Each subject is randomly allocated to either an AB sequence or a BA sequence. Subjects in the AB sequence receive treatment A at the first period and treatment B at the second period.
A model can be used to describe the standard 2 × 2 crossover design as follows:
Where
Yijk is the response of the ith subject in the kth sequence at the jth period,
subject i = 1, 2, ⋯, nk (ith subject in kth sequence)
period j = 1, 2 (First or second)
sequence k = 1, 2 (AB or BA)
The subject (
Sik) and error (
eijk) are independent and identically distributed random variables and have a normal distribution with mean 0 and variance of
σs2, and mean 0 and variance
σe2, respectively. This model
4) includes fixed effects such as the period effects (
Pj), the direct treatment effects (
Tj,k), and the carryover effects (
Cj-1,k). For example,
T1,2 represents the direct fixed effect of the treatment at period 1 in sequence 2 (Here, at the first period of the BA sequence), and
C2-1,1 is the residual effect carried over from the (2-1)
th period to the second period in sequence 1 (Here, the AB sequence). The carryover effect in the standard 2 × 2 crossover design can occur at the second period. The fixed effects at each period in each sequence are summarized as follows.
|
Sequence |
First period |
Second period |
|
AB sequence |
μ11 = μ + P1 + TA
|
μ21 = μ + P2 + TB + CA
|
|
BA sequence |
μ12 = μ + P1 + TB
|
μ22 = μ + P2 + TA + CB
|
Here,
μjk = E(Yijk), P1 + P2 = 0, TA + TB = 0, and CA + CB = 0.
Treatment emergent effects
In studies using a crossover design, elements such as carryover effect, period effect, sequence effect, and period-by-treatment interaction should be evaluated before testing the treatment effect. Even if effects other than the treatment effect were carefully considered and excluded in the research planning stage, it is necessary to check the carryover effect or the period effect before analyzing the treatment effect. After checking the above-mentioned effects are not absent, it is common to analyze the treatment effect. It is important in the crossover study planning stage is to design an analysis that does not become complicated and allow effects other than the treatment effect to influence the interpretation of the results [
5,
6].
Treatment effect
This refers to the direct effect of the treatment. In this article, it indicates the effects of A and B and
Tj,k in
Equation (1).
Period effect
The period effect implies that the effect of the same treatment received at two different periods is different for each period and corresponds to
Pj in
Equation (1). Since the first and second treatments are inevitably separated in time, an effect may appear depending on the measurement period, not the treatment. Therefore, when comparing the value obtained by subtracting the first period from the second period of the AB sequence with the value obtained by subtracting the value of the first period from the second period of the BA sequence
5), there should be no difference if there is no period effect.
Carryover effect
The carryover effect, which corresponds to
Cj-1,k in
Equation (1), refers to the effect of the previous treatment or the change caused by the first treatment continues until the next period and alters the effect of the next treatment. Rather than determining that there is no carryover effect by statistical testing, it is better to select a crossover design when the possibility of a carryover effect is medically unlikely or when the effect can be eliminated through a washout period. Analyzing for the period-by-treatment interaction is used to determine whether the two treatment effects are different in the two periods, and it is difficult to distinguish the carryover effect from the period-by-treatment interaction; therefore, the carryover effect and the period-by-treatment interaction are often treated as identical. However, depending on which parameters are included in the crossover design model, the carryover effect may be embedded in parameters other than the period-by-treatment interaction
6). In other words, it is difficult to analyze the carryover effect in the simplified 2 × 2 crossover design [
5]; therefore, it is important in the study planning stage to design such that the carryover effect does not occur. For example, there is a method to set a sufficient washout period until the treatment effect or change disappears. In the case of drug studies, a washout period is sometimes set at 3–4 times or more of the blood plasma elimination half-life.
Sequence effect
The fact that subjects are allocated to a particular sequence may affect the results. That is, when comparing the means of the dependent variables in the AB and BA sequences, there should be no difference if there is no sequence effect. This allows the assumption that there is no sequence effect by randomization in the AB/BA sequence. However, it should be noted that this assumption cannot be verified through statistical analysis [
6].
Randomization in crossover design
Randomization is performed to eliminate selection bias and to provide statistical evidence for quantitative evaluation. In parallel design, randomization to different treatment groups (A or B) can ensure independence between groups. However, in the crossover design, randomization is performed in sequence, that is, AB or BA sequence, so that virtually no independence between treatment groups is guaranteed. Therefore, as discussed above, it is necessary to test whether the treatment effect shown in the first period remains in the second period. The randomization method may be reviewed in the article of Lim and In [
7].
Other considerations
When planning the crossover design, to confirm the treatment effect, the carryover effect should not appear above all. The carryover effect can be found through data analysis, and when this effect is significant, it is difficult to interpret the treatment effect. Therefore, a protocol such as the above-mentioned washout period setting is an appropriate method to eliminate this effect. However, if the washout period is too long, the dropout rate may increase at the second period. In some cases, crossover studies may be impossible. For example, in the case of an acutely curable disease, if it is cured in the first period, there is no reason for the subjects to participate in the second period. Therefore, the crossover design is more suitable for chronic diseases than for acute diseases. These factors should be reflected in crossover design planning.
Statistical model and SAS code
Example
The example used below was published by Senn and Auclair [
8]. Thirteen pediatric patients aged 7-14 years were treated sequentially with two distinct bronchodilators, the newer drug formoterol (For, 12 μg) and the control drug salbutamol (Sal, 200 μg). Seven patients were randomized to the For-Sal sequence and six were randomized to the Sal-For sequence. An established washout period of at least 1 d was allowed between administration of the two drugs. Peak expiratory flow (pef, L/min) was measured 8 h after inhalation of each bronchodilator. The SAS code used in the following example was run using SAS 9.4 (SAS Institute Inc., USA) and SAS University Edition installed on a Microsoft Windows 10 (64-bit) operating system.
Data input into SAS
The full data entry is presented in
Fig. 1 of the Appendix. The SAS code for printing up to the first five lines (OBS=5) of all 26 lines of data and the results are as follows:
title “PEF data”;
PROC PRINT DATA = PEF(OBS=5);
RUN;
PEF data
OBS sequence subject period treat pef
1 For-Sal 1 1 For 310
2 For-Sal 1 2 Sal 270
3 For-Sal 4 1 For 310
4 For-Sal 4 2 Sal 260
5 For-Sal 6 1 For 370
Analysis of variance table to test other effects
Determining whether various effects other than the treatment effect appearing in this data can be easily accomplished through the analysis of variance table. The following code is used for the construction and execution of a general linear model to which analysis of variance is applied. Here, sequence represents For→Sal or Sal→For, the subject is a pediatric patient, and period represents the first period (1) or the second period (2). treat means cure using For or Sal. CLASS defines the variables to be used in the model, and MODEL is a code that specifies the independent and dependent variables.
PROC GLM DATA=PEF;
CLASS sequence subject period treat;
MODEL pef = sequence subject(sequence) period treat;
RUN;
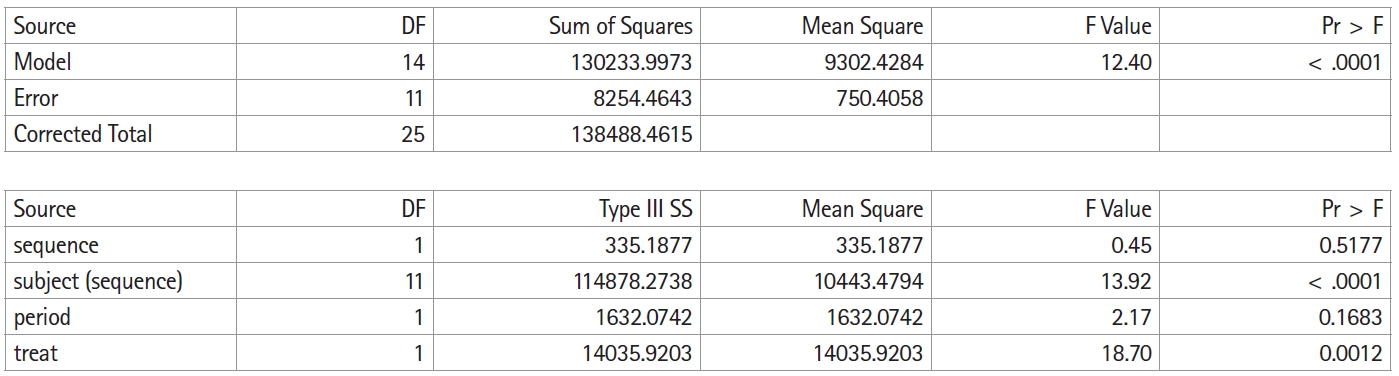
Fig. 2 shows the execution result of the above SAS code, and
Table 1 summarizes this result in an analysis of variance table. As mentioned above, it is not possible to separately confirm all effects or interactions because of the limitations of the simplified crossover design; hence, the carryover effect is inherent in other effects or interactions. In this crossover design model, the carryover effect is inherent in the sequence. Therefore, the result for the sequence is shown as carryover in
Table 1.
In the table of the sum of squares in
Fig. 2, the total sum of squares is divided into the between-subject sum of squares and the within-subject sum of squares. The between-subject sum of squares is again divided into the sum of squares for the carryover effect and the sum of squares for the residual. The within-subject sum of squares is divided into the sum of squares for the treatment effect, the sum of squares for the period effect, and the sum of squares for the residual. Neither the carryover effect ([F(1,11) = 4.84 > 0.45], P = 0.5177) nor the period effect ([F(1,11) = 4.84 > 2.17], P = 0.1683) is statistically significant.
Analysis of treatment effect
PROC MIXED DATA=PEF;
CLASS sequence subject period treat;
MODEL pef = sequence period treat;
RANDOM subject(sequence);
LSMEANS treat/PDIFF;
ESTIMATE 'Treatment' treat 1 -1 /CL ALPHA=0.05;
RUN;
The subject is included as a random effect through RANDOM subject (sequence). LSMEANS treat/PDIFF is a code that describes the P value for the difference between two treatments, and ESTIMATE 'Treatment' treat 1 -1 /CL ALPHA=0.05 represents the estimate of the treatment effect and 95% confidence interval.
After confirming that other effects do not appear through the analysis of variance table, the treatment effect can be analyzed using a linear mixed effect model (
Fig. 3). In pef, the average was 341.5 ml after inhalation of For and 294.9 ml after inhalation of Sal, and the pef was as high as 46.6 ml after inhalation of For (95% CI: 22.9–70.3 ml, P = 0.012).
Conclusion
The AB/BA design is a simplified form of the AA/AB/BA/BB crossover design introduced in clinical practice. It has many advantages, such as the ability of subjects themselves to reduce the influence of covariates by acting as a control group, and the higher power and statistical efficiency compared to those of the parallel design. However, there are also several limitations such as the difficulty in studying drugs with long half-lives, the requirement for subject stability even at different periods, administration of all treatments to one subject, and complicated processing of dropped or missing data. Therefore, it is necessary to understand the strengths and weaknesses of this study design and to apply an appropriate analysis method. It should also be noted that if a carryover effect occurs when using a crossover design, only the results of the first period can be explored.